filmov
tv
Evaluating a Quintic Polynomial from a Quadratic

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Evaluating a Quintic Polynomial from a Quadratic
Evaluating a Polynomial
Evaluating A Polynomial Expression in Four Ways
How To Factor a Polynomial to the 5th Degree #shorts
How To Evaluate a Polynomial Expression #shorts #shortsvideo #algebra
EVALUATE A POLYNOMIAL FUNCTION FOR A GIVEN VALUE | Algebra 2
Nested Scheme - Horner’s Method - Evaluating Polynomials
4 1 Evaluate Polynomial Functions
Evaluating a Cubic Polynomial Using a Quadratic in Three Ways
5.1 Evaluation & Graphing Polynomial Functions Alg 2 2020
Chinese Middle School Math Olympiad | Evaluate the polynomial with a cubic equation
How To Find The Polynomial Function From a Graph
Polynomial Expressions and Polynomial Functions
Step by Step Maths: Evaluation of a Polynomial Equation in Nested Form
Evaluating an Algebraic Expression Using a Polynomial
Evaluating the Polynomial x^5-29x
5 simple unsolvable equations
Evaluating a Polynomial Function (Example)
Can you factor this Quintic Polynomial | Factor of X^5 +X^4 + 1
Evaluating Polynomial Expressions | Math Olympiads
5.1 REMEDIATION Evaluating and Graphing Polynomial Alg 2
5.2: Evaluate and Graph Polynomial Functions, 1
polynomials super trick to find roots of cubic equation | factorisation trick
Solving Polynomial Equations By Factoring and Using Synthetic Division
Комментарии
 0:07:39
0:07:39
 0:04:58
0:04:58
 0:08:56
0:08:56
 0:00:39
0:00:39
 0:00:39
0:00:39
 0:05:27
0:05:27
 0:06:30
0:06:30
 0:02:13
0:02:13
 0:08:48
0:08:48
 0:20:30
0:20:30
 0:05:49
0:05:49
 0:10:04
0:10:04
 0:07:25
0:07:25
 0:03:55
0:03:55
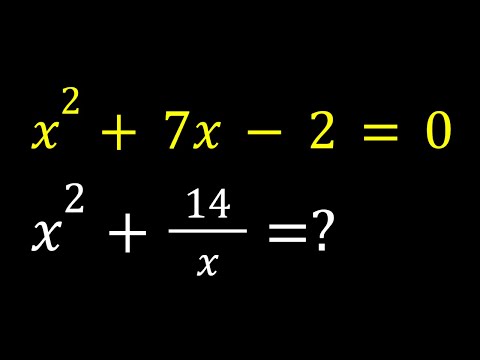 0:08:35
0:08:35
 0:08:38
0:08:38
 0:00:50
0:00:50
 0:00:55
0:00:55
 0:03:40
0:03:40
 0:00:56
0:00:56
 0:07:36
0:07:36
 0:19:21
0:19:21
 0:01:00
0:01:00
 0:14:19
0:14:19