AP Calculus AB UNIT 5 Analytical Applications of Differentiation

Here’s a brief description of each calculus topic from your list:

### 5.1 Using the Mean Value Theorem
The Mean Value Theorem states that if a function is continuous on a closed interval and differentiable on the open interval, then there exists at least one point \(c\) in the interval where the instantaneous rate of change (the derivative) equals the average rate of change over that interval. This theorem is fundamental for understanding how derivatives relate to function behavior.

### 5.2 Extreme Value Theorem, Global Versus Local Extrema, and Critical Points
This topic discusses the Extreme Value Theorem, which states that a continuous function on a closed interval attains both its maximum and minimum values. It distinguishes between global (absolute) extrema and local (relative) extrema and explains how critical points (where the derivative is zero or undefined) help identify these extrema.

### 5.3 Determining Intervals on Which a Function is Increasing or Decreasing
Students learn to analyze the first derivative of a function to determine intervals where the function is increasing or decreasing. If the first derivative is positive, the function is increasing; if negative, it is decreasing. This analysis helps in understanding the overall shape of the graph.

### 5.4 Using the First Derivative Test to Determine Relative (Local) Extrema
This topic involves using the first derivative test to identify local extrema. By examining the sign changes of the first derivative at critical points, students can conclude whether the function has a local maximum or minimum at those points.

### 5.5 Using the Candidates Test to Determine Absolute (Global) Extrema
The Candidates Test is a method for finding absolute extrema of a function on a closed interval. It involves evaluating the function at critical points and endpoints to identify the maximum and minimum values over that interval.

### 5.6 Determining Concavity of Functions over Their Domains
This topic focuses on using the second derivative to determine the concavity of a function. A positive second derivative indicates the function is concave up, while a negative second derivative indicates it is concave down. This understanding is essential for sketching graphs and analyzing function behavior.

### 5.7 Using the Second Derivative Test to Determine Extrema
Students learn to apply the second derivative test to classify critical points. If the second derivative at a critical point is positive, the function has a local minimum; if negative, it has a local maximum; and if zero, the test is inconclusive.

### 5.8 Sketching Graphs of Functions and Their Derivatives
This topic involves the process of sketching graphs of a function alongside its first and second derivatives. Students learn how the behavior of the derivatives (increasing/decreasing, concavity) influences the shape of the original function’s graph.

### 5.9 Connecting a Function, Its First Derivative, and Its Second Derivative
This topic explores the relationships between a function, its first derivative, and its second derivative. Students learn how these relationships provide insight into the function's behavior, including intervals of increase/decrease and concavity.

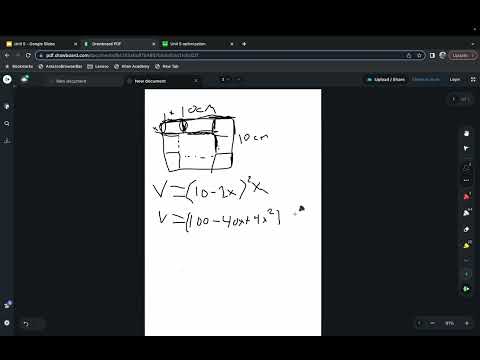
### 5.10 Introduction to Optimization Problems
Students are introduced to optimization problems, which involve finding the maximum or minimum values of functions within given constraints. This foundational topic prepares students for applying calculus techniques to real-world scenarios.

### 5.11 Solving Optimization Problems
Building on the previous topic, students learn methods to solve optimization problems systematically. This includes identifying the objective function, finding critical points, and using first and second derivative tests to determine optimal values.

### 5.12 Exploring Behaviors of Implicit Relations
This topic covers the analysis of implicit functions using techniques like implicit differentiation. Students learn to find derivatives, critical points, and concavity of functions defined implicitly, enhancing their understanding of more complex relationships between variables.

These topics provide a comprehensive foundation for understanding calculus concepts and their applications in analyzing functions and solving real-world problems.

I have many informative videos for Pre-Algebra, Algebra 1, Algebra 2, Geometry, Pre-Calculus, and Calculus. Please check it out:

/ nickperich

Nick Perich
Norristown Area High School
Norristown Area School District
Norristown, Pa

#math #algebra #algebra2 #maths #math #shorts #funny #help #onlineclasses #onlinelearning #online #study