Knuth Morris Pratt (KMP) String Search Algorithm - tutorial with failure function in Java

This tutorial explains how the Knuth-Morris-Pratt (KMP) pattern matching algorithm works. Animated examples are used to quickly visualize the basic concept. Then the source code of an implementation written in Java is discussed, along with its running time complexity.

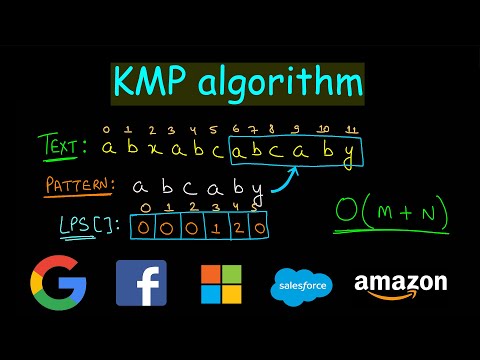
There are two parts to the algorithm. The first one creates a "failure function", which is nothing more than an array that holds the longest prefixes as they occur through out the pattern string. The main algorithm uses this prefix length array to calculate how much forward to shift the pattern string.

Source code written in Java:

The implementation is based on the pseudo-code taken from Wikipedia:

FAST PATTERN MATCHING IN STRINGS
DONALD E. KNUTH, JAMES H. MORRIS, JR. AND VAUGHAN R. PRATT

Written and narrated by Andre Violentyev

-----------------------------------------------------------------------------------------------------------------------------------------------
Errata (credit to @Achyut Sapkota):
My animation at 6:04 should have moved not by 2 but by 3 characters. By the way, at that point we'd also increment the pointer in the text to the next character. The source code (see above) is correct - once we get to index zero of the prefixLen array, which stores -1, we increment both the text and the pattern string pointers:
p = prefixLen[p];
if (p 'less than' 0) {
t++;
p++;
}
In the above example once we shift by 3, we essentially go "out of bounds" for the pattern string. The illustrations show that the first character, 'a', is at index 1 of the prefixLen array (not index 0, which is probably what is causing confusion since most programming languages use 0 based indexes for strings). So the formula works, it's just that, once we detect the "out of bounds" condition, we reset the pattern string pointer to the first character, and increment the text pointer by 1. In other words, we shift the pattern string so that its first character aligns with the next character in the text. This is what insures that each character in the text is examined at most twice.

[maridavies]

This is the best explanation of how the prefix array is constructed. Awesome job and thanks!

[mandeepsinghrr]

This channel honestly has the best explanation for all the difficult problems. The nlogn LIS implementation was too complex for me to understand, but then I stumbled upon this channel. The same goes for KMP! Amazing work! Really appreciate how you explain it in a simple manner!

[sloppyguy]

Even a sloppy guy like me would understand this explanation, well done!

I also like how you comunicate :)

[xiaoxiaoxiao]

The best explanation of the MIT version of KMP. Good job!!!
I learned the KMP algorithm through the 《Algorithm》which is public by Princeton University. The MIT version of KMP and Princeton's version is the two main version of the KMP algorithm.

[prasannakumarnaidu]

Thank you sir
After lot of confusion in understanding this algorithm you made it easy to understand . Hope you make many videos like this.

[junkaze]

This is far the best explanation and discussion of the KMP, thank you for saving my semester.

[irfanquader]

your explanation method (with the visualization ) and calm way of explaining really helped me understand the algorithm :)

[ram-ojij]

I watched other videos and it finally clicked with this video, thanks. All your other videos are produced very well and great.

[abdalla]

Wow this is the a way better explanation than the GFG article. Thanks

[vinayakf]

Just 1:44 into the video and got the ans I was long been pondering over, Thank you sir

[Japopo]

Your videos are the best for learning these algorithms. Much appreciated.

[danielsasse]

This was incredibly helpful for understanding the concepts behind the algorithm, Thank you!

[abelsimon]

thanks a lot for going through these classics, also your code looks simple and concise!

[juniperandspice]

i am so glad i stumbled onto this channel

[lukelyu]

The most efficient one out of those confusing videos

[AluSoft]

Hi Stable sort!

Please keep posting !!! You have the best videos I've ever seen!!!

[mohamedmusharaf]

Wow Sir. The explanation is really good!! Glad I've found your channel!!

[Prashantkumar-pnqq]

Very good and illustrative explanation!

[amitkumarprajapati]

Really appreciated your way of explanation sir

[mfrice]

Hi, I think there is another error at 5:23 in the animation. The shift should be (8-2)=6 instead of (9-3)=6. Although they happen to have the same results, the last 'c' in the pattern is a mismatch so it should not be counted in the matched length. Consider a modified example, the string is "abdxxxabdxxxabcde" and the pattern is "abdxxxabcde". The fist mismatch is at the 'c' in the pattern, and the lps of 'c' is 0. The shift should be the matched length 8 minus the lps of the second 'b' which is 2, which results in 6, rather than (9 - 0) = 9. Do you feel it make sense?