Understanding the Time Complexity of Recursive Fibonacci with Memoization

Explore how to mathematically prove the `Time Complexity` of the Fibonacci sequence using recursive functions and Memoization for optimization.
---

Visit these links for original content and any more details, such as alternate solutions, latest updates/developments on topic, comments, revision history etc. For example, the original title of the Question was: How to mathematicaly prove the Time Complexity of the recursive Fibonacci program with Memoization

If anything seems off to you, please feel free to write me at vlogize [AT] gmail [DOT] com.
---
Understanding the Time Complexity of Recursive Fibonacci with Memoization

When it comes to programming, especially in algorithm development, understanding the efficiency of your code is paramount. In this article, we will tackle the well-known problem of calculating Fibonacci numbers recursively. Specifically, we will delve into how to mathematically prove the Time Complexity of a recursive Fibonacci program using Memoization to optimize performance.

The Fibonacci Problem

The Fibonacci sequence is a classic example of a mathematical sequence where each number is the sum of the two preceding ones, often starting with 0 and 1. The Fibonacci sequence can be defined as follows:

F(0) = 0

F(1) = 1

F(n) = F(n - 1) + F(n - 2) for n 1

Performance of Standard Fibonacci Algorithm

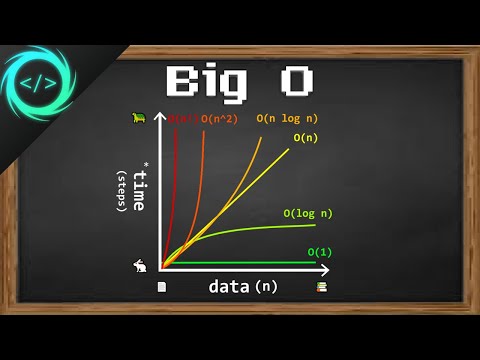
The conventional recursive method to compute Fibonacci numbers is simple but inefficient, resulting in a Time Complexity of O(2^n).

Why O(2^n)?

Let's see how we can come to this conclusion through a mathematical approach. The recursive function can be described by the following recurrence relation:

T(n) = T(n - 1) + T(n - 2)

When we apply this recursively, we find:

T(n) = 2T(n - 1) + c (where c is some constant time for computations)

Continuing this pattern, we can see that:

T(n - 1) = T(n - 2) + T(n - 3)

T(n - 2) = T(n - 3) + T(n - 4)

This yields an expanding tree of calls, which illustrates exponential growth in the number of function calls - leading to the O(2^n) complexity.

Introducing Memoization

To mitigate the inefficient nature of the standard recursive Fibonacci function, Memoization becomes a vital technique. This involves storing previously computed Fibonacci values so that we don't recalculate them.

Here’s how the optimized recursive method looks in Java:

[[See Video to Reveal this Text or Code Snippet]]

Analyzing Time Complexity with Memoization

After applying Memoization, the scenario changes significantly. The recursive relationship is still the same:

T(n) = T(n - 1) + T(n - 2)

However, instead of recalculating values multiple times, Memoization allows us to compute each Fibonacci number just once. The new time complexity can be derived as follows:

Each Fibonacci value is calculated exactly once.

The number of unique calls is linear with respect to n, making it T(n) = O(n).

Visualizing the Recursive Calls

To better understand this, consider the following illustrations representing the recursive call trees before and after Memoization.

Naive recursive implementation:

[[See Video to Reveal this Text or Code Snippet]]

With Memoization:

[[See Video to Reveal this Text or Code Snippet]]

Conclusion

In conclusion, by implementing Memoization, we transform the O(2^n) complexity of the naive Fibonacci algorithm into an efficient O(n). This not only optimizes performance for large n values but also illustrates the power of dynamic programming in reducing repeated calculations. Understanding the underlying math and mechanics of these complexities is vital for any programmer looking to enhance their coding skills.

By leveraging Memoization, we can confidently compute Fibonacci numbers with both accuracy and efficiency.