filmov
tv
Robert Bryant: Limits, Bubbles, and Singularities: The fundamental ideas of Karen Uhlenbeck

Показать описание
Abstract:
Ever since the Greeks, the challenges of understanding limits and infinities have fascinated us, ultimately leading to the development of calculus and much of modern mathematics. When does a limit exist and in what sense? How do we capture these notions in geometric and intuitive ways? Professor Uhlenbeck's work provides fundamental ideas for how to interpret situations in which one would like to take a limit of a set of geometric objects and interpret the result in useful ways. I will try to give a sense of what the challenges are and how Uhlenbeck's ideas provide answers to questions that mathematicians and physicists have been asking for many years. At the end, I will give a sense of how influential her work has been and continues to be.
The original title of the lecture is "Limits, Bubbles, and Singularities: An introduction to the fundamental ideas of Karen Uhlenbeck". We changed the title slightly in order to satisfy Youtube’s limitations on the length of a title.
Robert Leamon Bryant is an American mathematician and Phillip Griffiths Professor of Mathematics at Duke University, and specializes in differential geometry.
This lecture was held at The University of Oslo, May 22, 2019 and was part of the Abel Prize Lectures in connection with the Abel Prize Week celebrations. You can read more about the program, summaries and view all lectures on our website:
Program for the Abel Lecture 2019
1. "Some Thoughts on the Calculus of Variations" by Abel Laureate Karen K. Uhlenbeck, University of Texas at Austin, USA
2. "Solitons in Geometry" by professor Chuu-LianTerng, UC Irvine
3. "Limits, Bubbles, and Singularities: An introduction to the fundamental ideas of Karen Uhlenbeck" by professor Robert Bryant, Duke University
4. "An Attempt to Visualise Minimal Surfaces and Maximum Dimensions" by Matt Parker, Standupmaths
Ever since the Greeks, the challenges of understanding limits and infinities have fascinated us, ultimately leading to the development of calculus and much of modern mathematics. When does a limit exist and in what sense? How do we capture these notions in geometric and intuitive ways? Professor Uhlenbeck's work provides fundamental ideas for how to interpret situations in which one would like to take a limit of a set of geometric objects and interpret the result in useful ways. I will try to give a sense of what the challenges are and how Uhlenbeck's ideas provide answers to questions that mathematicians and physicists have been asking for many years. At the end, I will give a sense of how influential her work has been and continues to be.
The original title of the lecture is "Limits, Bubbles, and Singularities: An introduction to the fundamental ideas of Karen Uhlenbeck". We changed the title slightly in order to satisfy Youtube’s limitations on the length of a title.
Robert Leamon Bryant is an American mathematician and Phillip Griffiths Professor of Mathematics at Duke University, and specializes in differential geometry.
This lecture was held at The University of Oslo, May 22, 2019 and was part of the Abel Prize Lectures in connection with the Abel Prize Week celebrations. You can read more about the program, summaries and view all lectures on our website:
Program for the Abel Lecture 2019
1. "Some Thoughts on the Calculus of Variations" by Abel Laureate Karen K. Uhlenbeck, University of Texas at Austin, USA
2. "Solitons in Geometry" by professor Chuu-LianTerng, UC Irvine
3. "Limits, Bubbles, and Singularities: An introduction to the fundamental ideas of Karen Uhlenbeck" by professor Robert Bryant, Duke University
4. "An Attempt to Visualise Minimal Surfaces and Maximum Dimensions" by Matt Parker, Standupmaths
Комментарии
 1:02:09
1:02:09
 1:05:32
1:05:32
 0:03:29
0:03:29
 1:22:37
1:22:37
 1:03:49
1:03:49
 0:00:47
0:00:47
 0:00:05
0:00:05
 0:00:10
0:00:10
 0:00:18
0:00:18
 1:41:10
1:41:10
 0:50:02
0:50:02
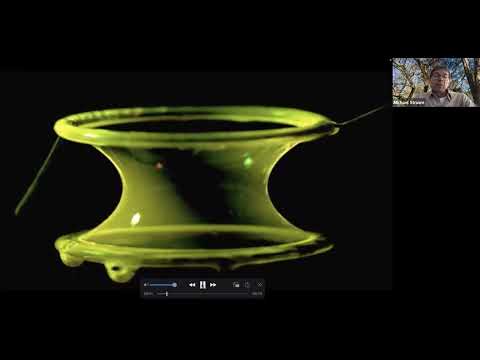 1:04:25
1:04:25
 0:02:25
0:02:25
 1:13:05
1:13:05
 0:23:10
0:23:10
 1:23:12
1:23:12
 0:00:31
0:00:31
 0:12:46
0:12:46
 0:03:06
0:03:06
 0:01:48
0:01:48
 0:51:08
0:51:08
 0:09:49
0:09:49
 1:00:49
1:00:49
 0:58:07
0:58:07