Continuity over an interval | Limits and continuity | AP Calculus AB | Khan Academy

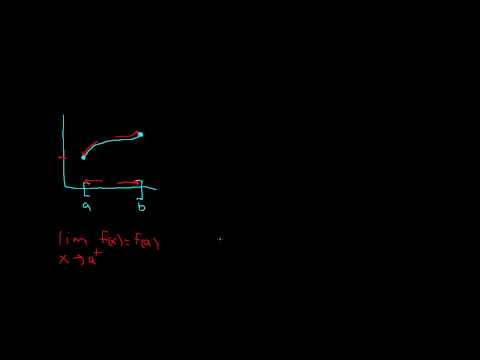
A function Ä is continuous over the open interval (a,b) iff it's continuous on every point in (a,b). Ä is continuous over the closed interval [a,b] iff it's continuous on (a,b), the right-sided limit of Ä at x=a is Ä(a) and the left-sided limit of Ä at x=b is Ä(b).

AP Calculus AB on Khan Academy: Bill Scott uses Khan Academy to teach AP Calculus at Phillips Academy in Andover, Massachusetts, and heÕs part of the teaching team that helped develop Khan AcademyÕs AP lessons. Phillips Academy was one of the first schools to teach AP nearly 60 years ago.

For free. For everyone. Forever. #YouCanLearnAnything

[Mimi]

How would you figure this out algebraically?

[johnferentoulaloum]

I need help in one question. There is an exercise that asks to prove this. Suppose f satisfies the conclusion of the middle value theorem (that in an interval [a, b] f takes every value between f(a) and f(b))and f takes on each value only once (suppose it means a 1-1 function) prove that the function is continuous at [a, b]. Ok it had an ε, δ contradiction proof which made no sense at all. Because it used the middle value theorem WITHOUT knowing that the function is continuous.Circular. Fact is the exercise looks totally wrong, because I can find any function of this kind which is NOT continuous and qualifies. You only have to find a function with no limit at certain x es. (Different - and + limit a x1, x2 etc). And it STILL is 1-1 and takes ALL VALUES between f(a) and f(b).It is a very interesting calculus book that I am studying but either I am missing something or there is a huge mistake. Any help?

[RobotNewgate]

Can anyone help me if
(negative infinity, 2] is continuous or not?