filmov
tv
Can You Pass Harvard College Entrance Exam?

Показать описание
Entrance examination and Olympiad Question in 2022. If you're reading this ❤️.
What do you think about this problem?
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
What do you think about this problem?
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
Can You Pass Harvard University Entrance Exam?
Can You Pass Harvard College Entrance Exam?
Can You Pass Harvard University Entrance Exam?
Can You Pass Harvard University Math Exam?
Can You Pass Harvard College Entrance Exam?
Can You Pass Harvard's Entrance Exam?
Can you Pass Harvard University Admission Exam with Ease ?
Can you Pass Harvard University Admission Interview ?👇
Can you Pass Harvard University Admission Interview ?
Can you Pass Harvard University Admission Entrance
Can You Pass Harvard University Entrance Exam ?
Can You Pass Harvard: University Entrance Exam?
Can you Pass Harvard University Entrance Interview ?
Can you Pass Harvard University Admission Exam ?
Can You Pass Harvard College Entrance Exam?
Can You Pass Harvard University's Entrance Exam?
Can you Pass Harvard University Admission Entrance
A Harvard University entrance examination|Algebra|can you pass this exam?
Can You Pass Harvard University's Entrance Exam Question ? 👇👇
Can you Pass Harvard University Admission Interview ?👇
Can You Pass Harvard's University Admission Interview Exam? Math Olympiad
Can you pass Harvard University Entrance Exam?| You should be able to solve this
Can You Pass Harvard's (University) Entrance Exam?? x^2 -x^3=80.
Can You Pass Harvard's University Admission Interview?
Комментарии
 0:10:46
0:10:46
 0:08:12
0:08:12
 0:10:02
0:10:02
 0:14:00
0:14:00
 0:06:24
0:06:24
 0:07:28
0:07:28
 0:15:23
0:15:23
 0:06:20
0:06:20
 0:08:02
0:08:02
 0:08:55
0:08:55
 0:00:57
0:00:57
 0:09:34
0:09:34
 0:11:08
0:11:08
 0:16:47
0:16:47
 0:12:09
0:12:09
 0:05:13
0:05:13
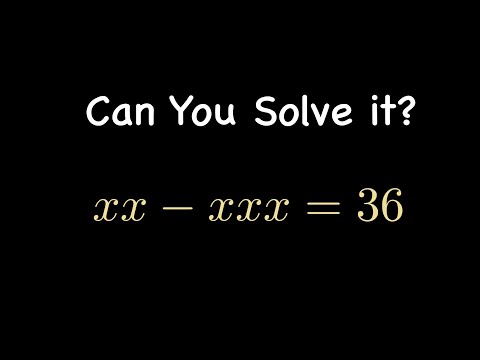 0:07:38
0:07:38
 0:09:33
0:09:33
 0:11:00
0:11:00
 0:08:25
0:08:25
 0:10:56
0:10:56
 0:03:13
0:03:13
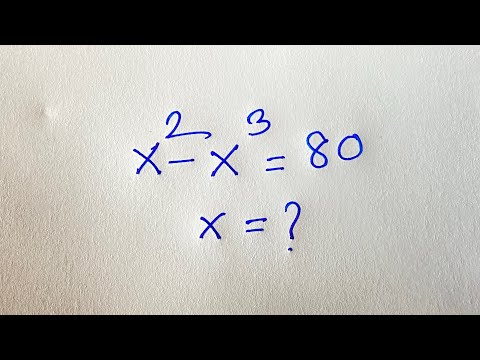 0:09:53
0:09:53
 0:08:29
0:08:29