filmov
tv
Session 7: Exact Differential Equations along with examples.(See pinned comment)
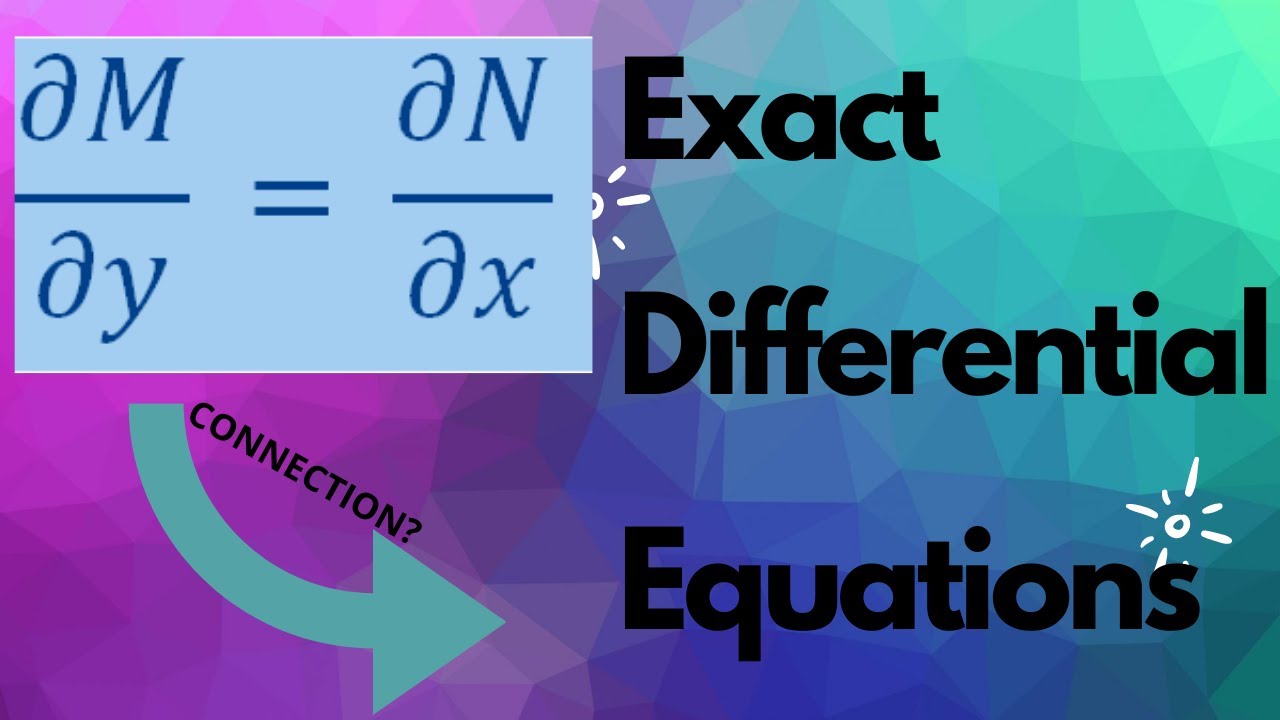
Показать описание
In this video, we will see what do we mean by the total derivative of a function. Then we will see what do we mean by the Exact differential equation along with some examples. Then we will see a theorem that gives the necessary and sufficient condition for a differential equation to be exact. At the end, we will see an example/algorithm to find the solution using the exactness method.
===============================
Link for Variable separable method:
================================================
Link for reduction to the variable separable method:
===============================
Link for Variable separable method:
================================================
Link for reduction to the variable separable method:
Session 7: Exact Differential Equations along with examples.(See pinned comment)
EXACT DIFFERENTIAL EQUATION SHORTCUT TAGALOG PROBLEM 7
Engineering Mathematics | Exact Differential Equation
Lec7/First Order ODEs/Exact Differential Equations
First Order Differential Equations - Exact Differential Equations | Math with Janine
DIFFERENTIAL EQUATION:EXACT DE Tutorial
Exact Differential Equations
Differential Equations - 09 - Exact Equations
🎯GATE & ESE 2025|| EC/EE/IN|| ANALOG|| Question Practice Series|| Op-Amp⌛#gate2025 #gatepreparat...
Exact Differential Equation
Exact Differential Equation | Part -1 |GATE 2022-23 | Mathematics| Pallav Gour|The Great Hall - Gate
Exact Differential Equations
Session 9: Integrating Factor to convert non exact differential equation into Exact differential eq.
That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...
Method7: Exact Differential Equation Form by AMMAJI RAO DUPPADA
|| Exact & Non Exact Differential Equations || #lecturecadre #mastercadre #dsssb #htet #diferent...
Exact Differential Equations
Differential Equation - Part 9 (Exact Differential Equation)
Exact Differential Equation | L 60 | Differential Equation | Engineering Mathematics 2.0
Exact Differential Equation | dy/dx = (-4e^(x)cos(y) - (y^2)/x)/(-4e^(x)sin(y) + 2y ln(x) + 5y^2)
Exact Differential Equations | Differential Equations | Mathematics | Target JEE 2019 | Day 103
011 Solving Differential Equations - Reducing to Exact Form
Exact Differential Equation | GATE 2022-23 | Mathematics | Pallav Gour | The Great Hall - Gate
#3 Example on Exact Differential Equations
Комментарии
 0:19:03
0:19:03
 0:03:53
0:03:53
 0:07:25
0:07:25
 0:18:07
0:18:07
 0:08:22
0:08:22
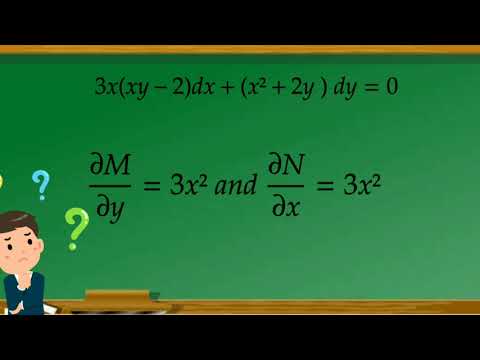 0:03:56
0:03:56
 0:18:19
0:18:19
 0:21:07
0:21:07
 2:00:11
2:00:11
 0:12:11
0:12:11
 0:26:36
0:26:36
 0:07:08
0:07:08
 0:13:07
0:13:07
 0:00:19
0:00:19
 0:16:41
0:16:41
 0:26:39
0:26:39
 0:36:14
0:36:14
 0:29:40
0:29:40
 1:20:35
1:20:35
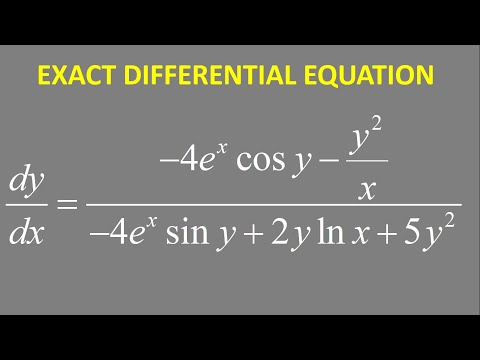 0:01:09
0:01:09
 0:41:43
0:41:43
 0:12:53
0:12:53
 0:31:41
0:31:41
 0:13:52
0:13:52