Deterministic Finite Automata (Example 4)

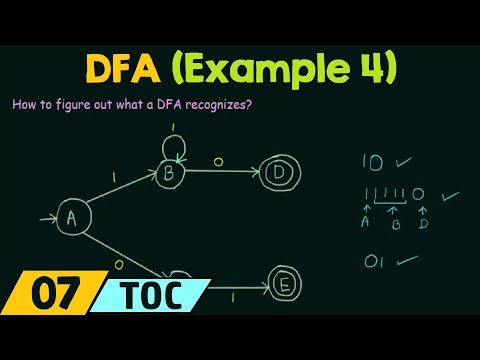
TOC: An Example showing how to figure out what a DFA recognizes. This lecture shows how to figure out what a DFA recognizes and how to complete a DFA using a Dead State.

Music:
Axol x Alex Skrindo - You [NCS Release]

#TheoryOfComputation #TOCByNeso #DeterministicFiniteAutomata #DFA #AutomataTheory

[Laeyz]

'whatever happens in dead state, stays in dead state.' sounds familiar.

[mohammad_a_razeq]

This channel is really beautiful and very useful, thank's for your effforts

[curtispatrick]

Great aid, but I think this one has a couple of problems. 1. (D) should transition to self on {0, 1} because you've matched on the '1 followed by 0'. 2. (C) on {0} should transition to another state, (F) because while '00' will never match the '01' rule, it *might* match the '1 followed by 0' rule. (F) would transition to itself (F) on '0', but transition to (B) on 1.

Of course, I could be wrong. I'm here because I'm looking at ANTLR and it talked about DFA and NFA and I have found these tutorials really useful, easy to consume, and easy to remember.

[arpitadaspoddar]

I think the language will be like dfa accepts the string 01 or a string starting with atleast one 1 followed by 0. other wise the string 010 has atleast one 1 followed by 0, but 010 is not accepted according to dfa.

[nehatadam]

The state transition diagram is not complete. DFA is a machine for which every state must contain transition for every input symbol and single transition per input symbol.

[NewtonMD]

A DFA must have a transition for all symbols for all states. That was not a DFA from the beginning, and adding states to the automaton changes it from the original, which was not a dfa

[vishalkumarjha]

Here, the string 1111....10 (at least one 1 followed by 0 is not assumed to be a sub string, it just is at least one 1 followed by one 0. )

For instance, 1110 will be accepted . But 11101 or 11100 will be rejected. So, stage D has to transition to Stage X to ensure rejection of the above mentioned strings. If stage D transitions to D itself, then 11101 and 11100 will both be accepted .

If the case was that at least one 1 followed by a 0 was a sub-string(for example 11100 or 11101) then D should have transitioned to itself on 0 and 1 .


The question is not about 01 or 111...10 being sub-strings .

It either exactly has to be 01 or (n number of 1s followed by a 0, where n=1, 2, 3....).


So, basically
1110 accepted.
11101 rejected.
11100 rejected.
01 accepted.
010 rejected.
010101 rejected .

As we can see, the examples which have been rejected above have 1110 and 01 as sub strings, but since they are not the complete strings, they are rejected.
That's the demand of the question.


Although, there's a problem of clarity in the statement. The fact that it has not to be a sub string could have been stated better.

L = {Accepts the string 01 or a string of at least one 1 ended by exactly one 0.} This could have been a more clear representation of the DFA.

[haoranchang]

I would say D should not go to the dead state. Because when you are in state D, which means there IS at least one '1' followed by a 'zero'. So no matter what the rest of the string looks like, it should be accepted.

[Ali_Alhajji]

So what this DFA does is :
1) Accepts 01
2) Accepts all strings that start with a sequence of 1s followed by a single 0.

[mohammadvasimbaig]

00:09 Determining what the given DFA recognizes

01:33 Two types of strings are accepted

03:00 The DFA recognizes the string 0 1 or a string with at least one binary digit 1 followed by a 0.

04:35 Deterministic Finite Automata (DFA) accepts strings of at least 1 binary digit 1 followed by a 0.

05:59 The DFA does not have a place to go for certain inputs

07:16 Dead state is a state in a DFA that leads to non-accepted strings.

08:29 Implementing a DFA

09:53 Not having a terminating state in a DFA leads to a dead state

Crafted by Merlin AI.

[IndieDeveloperGuy]

So what this DFA does is :
1) Accepts 01
2) Accepts all strings that starts with 1 and ends with 0

[mayureshwadgaonkar]

Why haven't we applied a self loop for c if it's gets input 0..like we did for b for input 1

[anuragporwal]

For DFA, at C there should be a input '0', this is NFA

[hectorg]

I freaken love you and this channel for this content!

[StudyArtist-plbn]

00:07 Determining the language recognized by a DFA
01:28 Deterministic Finite Automata in action
02:56 DFA recognizes 0 1 or a string with at least one 1 followed by 0
04:31 Illustrating the acceptance of binary strings by a DFA
05:53 DFA transition fails for certain input strings
07:13 Introduction to Dead State in DFA
08:24 Deterministic Finite Automata example 4
09:51 Not terminating state = dead state

[christiana.collamar]

I think the constructed DFA only accepts a subset of strings defined by the language, e.g. the string 010 is not accepted even though it should be since it's a string with at least one 1 followed by a 0. To make the DFA accept such strings, I think these transitions must be followed:
δ(E, 1) = B
δ(D, 1) = B
δ(X, 1) = B

[shouvikdutta]

01 and string starts with 1 and ends with 0??

[sriman]

Sir I think it is not a DFA because in this all states not covers all transitions

[rajeevdey_]

What happen if '1111' string goes?🙄
According to me it will not reach upto final state. Means it is not acceptable?

[mymysf]

What a plot twist! The X-state is like the zombie of the states!!