Graph of cosechx|Graph of Hyperbolic cosecant function|Main point of graph|Maths Online|Shah Hussain

Learn Mathematics By Shah Hussain
Graph of cosecanthx || Graph of hyperbolic cosecant function || Maths Tricks || Shah Hussain

Introduction to the Hyperbolic Cosecant Function
Defining the hyperbolic cosecant function
The hyperbolic cosecant function is an old mathematical function. It was first used in the articles by L'Abbe Sauri (1774).

This function is easily defined as the raciprocal of the hyperbolic sine function.
cosecanthx=1/sinhx
cothx=1/ [exp(x)-exp(-x)]

This function can also be defined as reciprocal to the hyperbolic sine function:

cosecanthx=1/sinhx

▪️Graphical representation
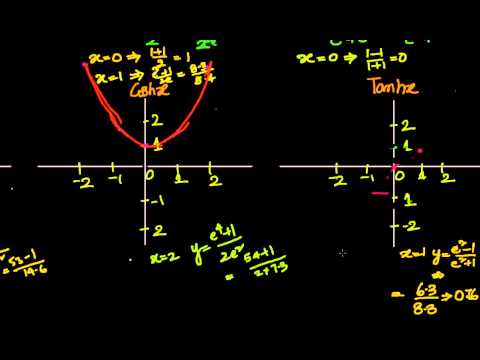
The graph of the hyperbolic cosecant function is shown in the video. Unlike the trigonometric cosecant, the function is not periodic(Aperiodic)
Hyperbolic cosecant is antisymmetric function defined everywhere on real axis, except its singular point 0 — so, function domain is (−∞, 0)∪(0, +∞).

☆FORMULAE OF COSECANTHX:
▪︎cosechx=1/sinhx
▪︎cosecanthx=1/(e^x-e^-x)
▪︎cosecanthx=1/sinhx
☆DOMAIN OF FUNCTION :
Set of all real numbers except zero
or (−∞, 0)∪(0, +∞).
or R-{0}
☆RANGE OF FUNCTION:
Set of all real numbers except zero
or (−∞, 0)∪(0, +∞).
or R-{0}

☆NATURE OF FUNCTION :cosecant hyperbolic function is an odd function by nature. i.e
▪︎cosechx(-x)=-cosehx
▪︎ coth(-x)=1//e^-x-e^x) or
▪︎ coth(-x)=-1/(e^x-e^-x)=-cosechx
☆GRAPH OF FUNCTION:
▪︎Graph of cosecant hyperbolic function is smooth curve within the domain of function
▪︎Graph of cosecant hyperbolic function is decreasing function
▪︎Graph of cosecant hyperbolic function is unbounded
☆SYMMETRY OF GRAPH :
The graph of cosecant hyperbolic is symmetric about the origin because it is an odd function. i.e
cosech(-x)=-cosech(x)
☆DERIVATIVE OF FUNCTION:
Derivative of cosechx is -cosechx cothx
i.e (cosechx)"=-cosechx cothx
☆DECREASING FUNCTION:
Hyperbolic cosecant function is decreasing function .
☆ASYMPTOTES OF FUNCTION:
Equation of Horizontal Asymptotes of cosecx is y=0 and Equation of vertical asymptotes is x=0
☆APERIODIC FUNCTION:
All hyperbolic trigonometric functions are
aperiodic (non periodic)
so cosecant hyperbolic function is also aperiodic(non-periodic)
☆EULER'S CONSTANT: e is called Euler's constant also
2《 e 《3 which is approximately =2.718281which is an irrational no.
also "π" is an irrational number and basically it is ratio of circumference of circle to diameter of circle. i.e π =Circumference/Diameter
LINKS:

☆Whatsapp: [phone]
.............................................................................
.............................................................................

Thank you so much😊😊❤❤
It gives me immense pleasure for your valuable suggestions and comments.
#SHAH_HUSSAIN#HYPERBOLIC_FUNCTION#TRIGONOMETRY#SECX#TANX#SINX
#COSX#TANGENT#SINX#PROPERTIES_COSX
#COSX_PROPERTIES#COSX_TABLE
#FUNCTION#DOMAIN#RANGE#PERIOD
#FREQUENCY#AMPLITUDE#PHASE_SHIFT
#GRAPG#SYMMETRY#SMART_TRICKS
#SHORT_CT#TIPS#AMPLITUDE#GRAPH#DOMAIN#RANGE#FUNCTION#PHASE_SHIFT#PERIOD
#FREQUENCY#SYMMETRY#SMOOTH_CURVE
#SECX#COSECX#SINX#ASYMTOTES#MATHS
#VERTICAL_ASYMTOTES#GRAPH#TANX
#ONLINE_LECTURES#MATHS_FORMULAE
#FUNCTION#FUNCTION_DOMAIN
#FUNCTION_RANGE#AMPLITUDE
#TRIGONOMERTIC_FUNCTIONS#HYPERBOLIC
#FUNCTION#APERIODIC#BOUNDED_FUNCTION

[fatimamumtaz]

Sir ji your method of teaching is admirable

[EhtshamUlHaqq]

MashAllah Sir G Great Job Allah Pak Ap Ko Hmesha Slamat Rakhain or Mzeed Traqi Ata Farmayn !! AmeeN.

[aminaabbas]

Superb sr g Allah krey ap mazeed progress kren Ameen

[MuhammadMuhammad-iure]

It gives me immense pleasure to see your determination.
😇keep presenting ...

[imranusman]

Well explained...👍😊
Your effort is inspiring...😊

[MuhammadMuhammad-iure]

Nice quotation🌸🌼🌸.
"The second name of beauty is mathematics."
Your work is also beautiful.

[yumathacademy]

Manage Board skills during lecture is admirable...😃

[yumathacademy]

Can we say this graph is continuous that's why it's Unbounded??