filmov
tv
Find the Value of k in a Quadratic Equation so that One Root is Half the Other
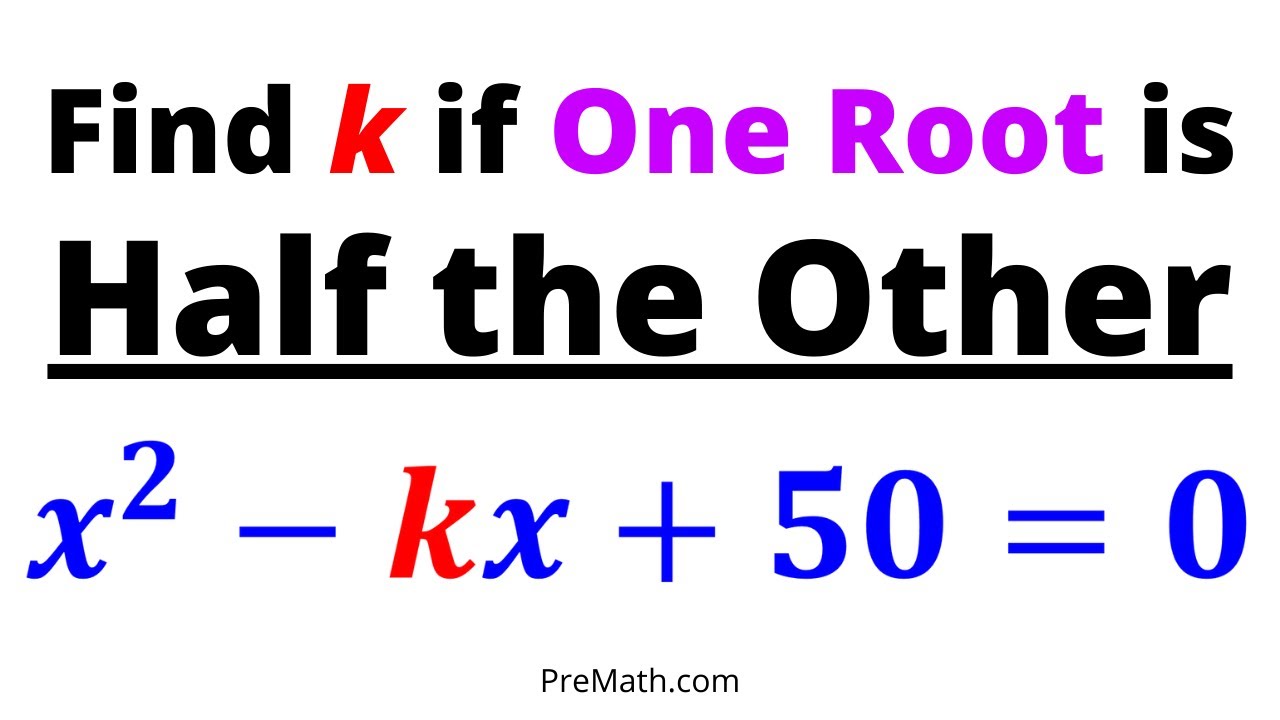
Показать описание
Find the Value of K for which the Quadratic has Equal Roots - Quick and Simple Explanation
Find the Value of k in Quadratics for Different Scenarios Involving Roots | Step-by-Step Explanation
Find the Value of k for this Quadratic Equation - Quick & Simple Explanation
Find the value k that makes the function continuous
How to Find Value of k when Two Linear Equations have Infinitely Many Solutions - Simple Tutorial
Find the Value of k in Quadratic Equations when One Root is Given | Step-by-Step Explanation
Find the value of k if 1³+2³+……+k³ = 44100
Find the values of k which give, one Solution, no Solution, or infinitely Many Solutions
K.Givens- Boy, Stop It 🤡 (Official Music Video) 2024
Find the Value of k when Two Quadratic Equations have ONE Common Root - Quick & Easy Explanation
Find all Values of K so Augmented Matrix is a Consistent System | Linear Algebra Exercises
Find the value of k so that the Function is a Probability Density Function
FIND THE VALUE OF K THAT MAKES THE FUNCTION CONTINUOUS
Find the Value of k in a Quadratic Equation so that One Root is Half the Other
Find the Value of K for which the Quadratic has Equal Roots - Quick and Simple Explanation - Tagalog
Find the Value of K to make a Perfect Square Trinomial | Step-by-Step Explanation
Find the Value of k and Second Solution if a Quadratic has only ONE ROOT | Step-By-Step Explanation
Find the Value of K given a specific remainder when dividing
Determine the value of k for trinomial to be a perfect square
ARITHMETIC SEQUENCE: SOLVING FOR THE VALUE OF K.
Probability finding the value of k example(PART-1) by EASY MATHS EASY TRICKS
Finding the Value of K That Makes a Function Continuous (Example)
Determine which values of k will give, one Solution, no Solution, or infinitely Many Solutions
Find the value of k if x=2 y=1 is a solution of the equation 2x+3y=k | How to find value of k
Комментарии
 0:03:35
0:03:35
 0:10:01
0:10:01
 0:05:03
0:05:03
 0:02:50
0:02:50
 0:06:26
0:06:26
 0:06:17
0:06:17
 0:03:18
0:03:18
 0:11:55
0:11:55
 0:02:36
0:02:36
 0:04:12
0:04:12
 0:05:12
0:05:12
 0:04:50
0:04:50
 0:03:21
0:03:21
 0:07:08
0:07:08
 0:02:46
0:02:46
 0:04:59
0:04:59
 0:05:04
0:05:04
 0:03:50
0:03:50
 0:03:22
0:03:22
 0:05:08
0:05:08
 0:07:53
0:07:53
 0:03:10
0:03:10
 0:13:41
0:13:41
 0:01:37
0:01:37