filmov
tv
This infinite series is crazy!
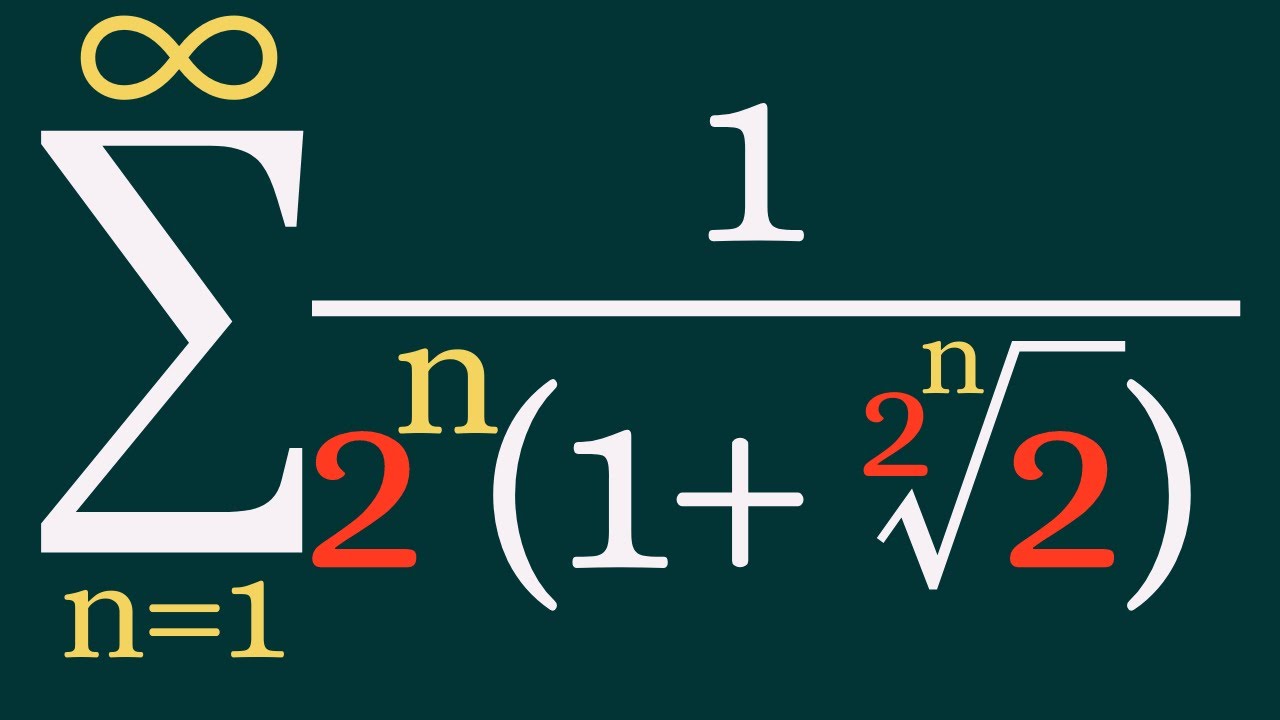
Показать описание
We look at a nice infinite sum.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
This infinite series is crazy!
Ramanujan's infinite root and its crazy cousins
What's this infinite sum?
How An Infinite Hotel Ran Out Of Room
Ramanujan's Magnificent Formula For π #ramanujan #mathematics #maths
「 Infinite Void 0.2s 🥵」- God Speed ⚡ #anime #jujutsukaisen
From 0 to ABSOLUTE INFINITY Ω
Be Lazy #shorts
The Beauty of Mathematics #inspiration #themanwhoknewinfinity
When mathematicians get bored (ep1)
Infinity calculator.
Infinite Village Seed
Wanda has all the power of infinity stones #multiverseofmadness #wanda #shorts
Mathematician Explains Infinity in 5 Levels of Difficulty | WIRED
Something Strange Happens When You Keep Squaring
Infinite chocolate trick explained
5 Unusual Proofs | Infinite Series
Proving Pick's Theorem | Infinite Series
'So close 🤏🏼,yet so far ♾️' Explanation and code in description #maths #satisfying #adhd #...
How Infinity Works (And How It Breaks Math)
Others in the Infinity Castle meanwhile⚡Zenitsu | Demon Slayer Season 4 Episode 8 Edit #demonslayer...
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
How to steal chocolate for free - infinite chocolate
Every Student Should See This
Комментарии
 0:16:59
0:16:59
 0:17:17
0:17:17
 0:00:31
0:00:31
 0:06:07
0:06:07
 0:00:37
0:00:37
 0:00:40
0:00:40
 0:00:58
0:00:58
 0:00:44
0:00:44
 0:00:59
0:00:59
 0:00:37
0:00:37
 0:00:13
0:00:13
 0:00:10
0:00:10
 0:00:16
0:00:16
 0:24:44
0:24:44
 0:33:06
0:33:06
 0:00:48
0:00:48
 0:08:44
0:08:44
 0:11:47
0:11:47
 0:01:00
0:01:00
 0:19:42
0:19:42
 0:00:18
0:00:18
 0:00:38
0:00:38
 0:00:15
0:00:15
 0:00:58
0:00:58