filmov
tv
A Nice Olympiad Exponential Problem.
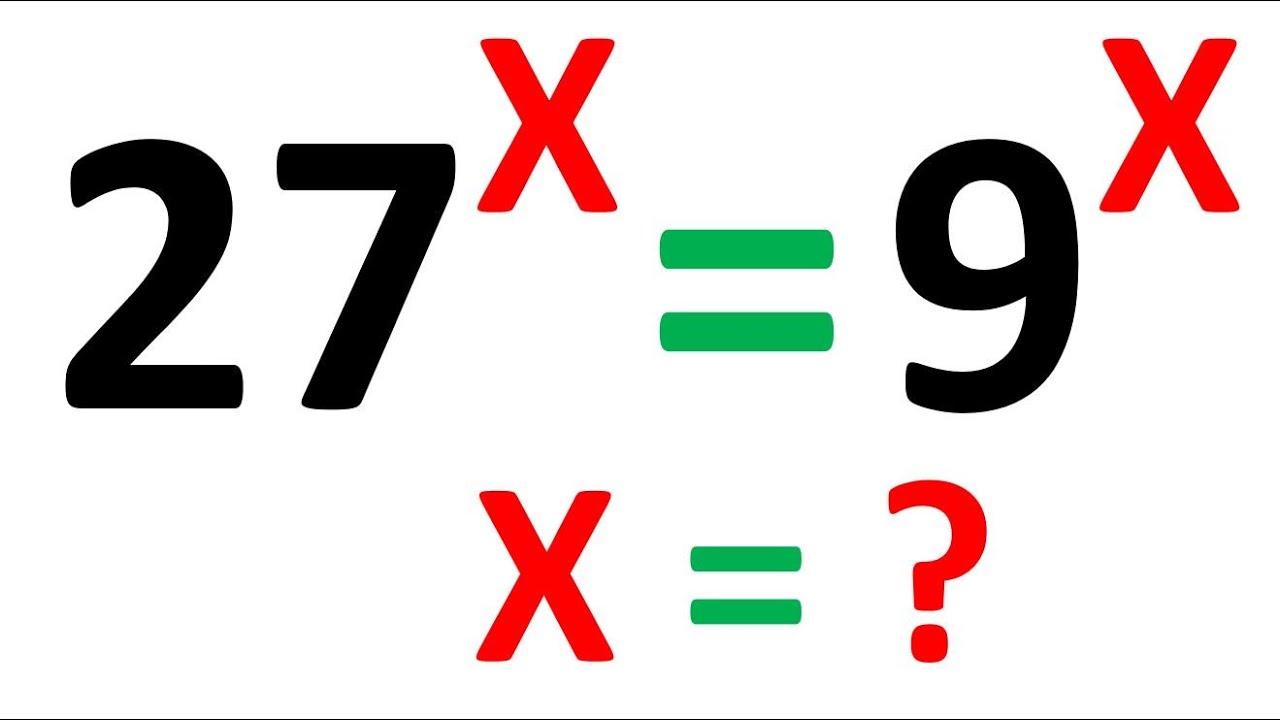
Показать описание
Dear Friends 😍
Welcome to your channel. I hope you are happy, well and safe 😊 Today we will solve this math problem. Please feel free to comment if you have better ideas/methods to find the answer. If you think you gained some knowledge and want to support me, please "Like" the video and "Subscribe" the channel.
Thank you all 🙏❤️.
#exponents #maths #algebra #olympiad
Welcome to your channel. I hope you are happy, well and safe 😊 Today we will solve this math problem. Please feel free to comment if you have better ideas/methods to find the answer. If you think you gained some knowledge and want to support me, please "Like" the video and "Subscribe" the channel.
Thank you all 🙏❤️.
#exponents #maths #algebra #olympiad
A Nice Olympiad Exponential Problem...
A Nice Math Olympiad Exponential Equation 3^x = X^9
Russia | A Nice Algebra Problem | Math Olympiad
Mexico - A Nice Math Olympiad Exponential Problem
A Nice Olympiad Exponential Problem | How to Solve?
A Nice Olympiad Exponential Problem
A Nice Olympiad Exponential Equation: find X=?
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
United Kingdom - A Nice Exponential Equation | Math olympiad Question
A nice mathematics algebra exponential problem | Olympiad Question| m=?
A Nice Olympiad Exponential Problem | Can You Solve This?
Japanese Math Olympiad Problem | A Nice Math Problem : Comparison
A nice olympiad exponential problem maths olympiad
USA | Nice Olympiad Exponential Equation: solve for a!!👇
USA Nice Olympiad Exponential Equation: solve for a!
A Nice Olympiad Exponential Problem
A Nice Math Olympiad Exponential Problem | Find the value of x, If 5^x+5^x=150
Nice Olympiad Exponential Equation: find a
A nice Exponential problem 😍 ll Math Olympiad #maths #olympiad #exponential
Japanese|A Nice Math Olympiad exponential problem|solve for x.
A nice mathematics algebra exponential problem | Olympiad Question| a=?,b=?
China | A nice Olympiad Exponent | Find x in this Problem
Global North | A nice Olympiad Exponent | Solve for x in this Problem
A Nice Olympiad Exponential Problem Solving By Math Tutor Jakaria✍️A Nice Olympiad Algebra Problem🔥...
Комментарии
 0:05:08
0:05:08
 0:02:34
0:02:34
 0:15:45
0:15:45
 0:08:36
0:08:36
 0:07:41
0:07:41
 0:04:12
0:04:12
 0:08:04
0:08:04
 0:00:52
0:00:52
 0:09:19
0:09:19
 0:11:21
0:11:21
 0:14:40
0:14:40
 0:04:15
0:04:15
 0:05:21
0:05:21
 0:08:09
0:08:09
 0:08:05
0:08:05
 0:06:20
0:06:20
 0:06:00
0:06:00
 0:08:26
0:08:26
 0:02:36
0:02:36
 0:12:54
0:12:54
 0:11:37
0:11:37
 0:11:04
0:11:04
 0:11:14
0:11:14
 0:08:34
0:08:34