Volume of a Cone - An Unusual Proof

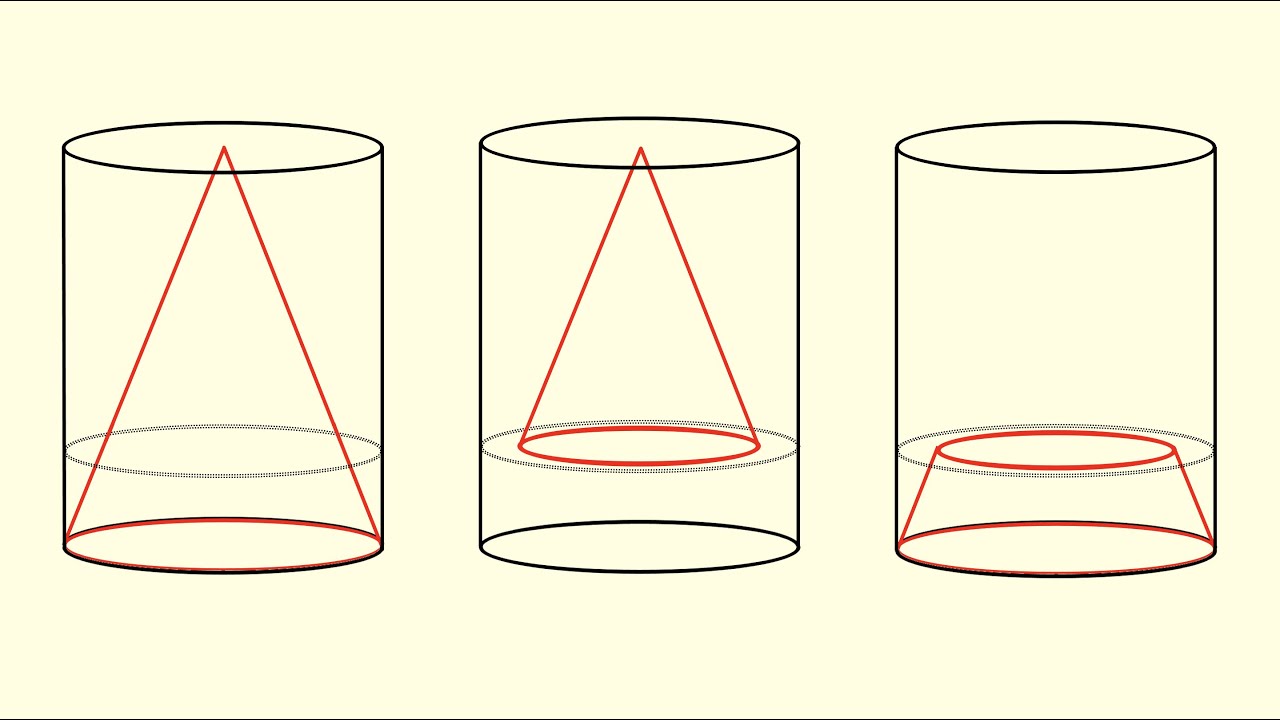
We look at an interesting derivation of the formula for the volume of a (right circular) cone. Adapted from the proof in this article:

Pargeter, A. (1976). The Volume of a Cone. The Mathematical Gazette, 60(413), 203-203. doi:10.2307/3617479

00:00 Intro
00:11 Setup
00:56 Idea of the proof
03:05 Proof

[onlyonecjb]

Love it and that you share this. I think this is perfect length of video for people to follow the all the steps especially regardless of their expertise.

[GiridhurSriram]

Amazing proof! What is the basis for the first assumption : "Cone Volume is proportional to Cylinder Volume"?

[oribadyl]

I love the proof, we've proven it in our calculus class when we started intergrals.

[MrRyanroberson]

1:33 you can prove this assumption from simple geometry: all cones nested in cylinders can be uniformly transformed into one another by scaling the cylinder base and height independently. The height uas linear proportionality, and the base quadratic proportionality. Furthermore: cutting off the topmost cone from a cone, by the definition of a cone, is always uniformly similar; which is to say: the volume of the cone in Vc' is exactly (n-1)^3/n^3 the area of the original.

[emanuellandeholm]

I have fond memories of my seventh grade math teacher asking the class for the formula of the volume of a conic solid in terms of base area and height and I raised my arm and blurted out 1/3 A h on pure intuition. She was so impressed! :D

Edit: Beautiful proof tho. Never seen that one before!

[jhuyt-]

Nice proof! How do you deal with the case n <= 1?

[akmchem_advanced]

Very interesting proof-- does not require very high level knowledge of integral calculus. Really enjoyable.

[txikitofandango]

There's something about derivatives, discrete ones, baked into the concept of n³ - (n - 1)³. The factor of 3 materializes in this derivative, which is nothing but a result of the Binomial Theorem.

[mienzillaz]

I love it. I always had trouble to visualize that 1/3 in formula.

[andrewdsotomayor]

Slightly shorter*
Very nice video, never seen this proof before!

[rivkahlevi]

Why restrict yourself to a cone? Doesn't this hold for any shape of base?

[vanphi]

Wow i cant believe this exist o.O. So brilliant !!! Keep it up !!!

[humanaccount]

that was the coolest proof. Thank u. Plus no music, this type of math is supposed to be interesting not accompanied with obnoxious cooking music

[MichaelRothwell]

A beautiful proof. Of course, there has to be a limit in the proof somewhere...

[mathcanbeeasy]

I don't think is ok to take axiomatic that the volume of the cone is always the same fractions of the volume of the cilinder. In other words, why that k is always the same constant? Ok, we know that k is always 1/3, but is something like we use a part of something that we want to prove, in this case the fact that k is always the same constant. Maybe if we double the cilinder, the volume of cone will be 1/4 of the volume of cilinder?! So, I think you must prove that k is always the same. You can't say that k is always the same becouse is 1/3, becouse you use k is allways the same in demonstration of k=1/3.
But, I found your channel one of the most interesting and you are a genius of how math can be so beautiful and easy if it is explained by someone like you. I love your stile. ❤️

[Kyrelel]

Interesting, but one step seems to have been glossed over.
Where is the source showing that the new radius is ((n-1)/n)r ?

[worldnotworld]

Great – but what does he keep calling the base part of the cone? The "crustin?" I can't figure it out...

[cmilkau]

The same proof works for higher dimensions, nice

[robertphillips]

What if my cone is not infinitely tall?

[rafiihsanalfathin]

What if its not a perfect cone but still hold the property of the limit?, then all non-perfect cone formula is still 1/3.pi.r^2