The Reduced Phase Space

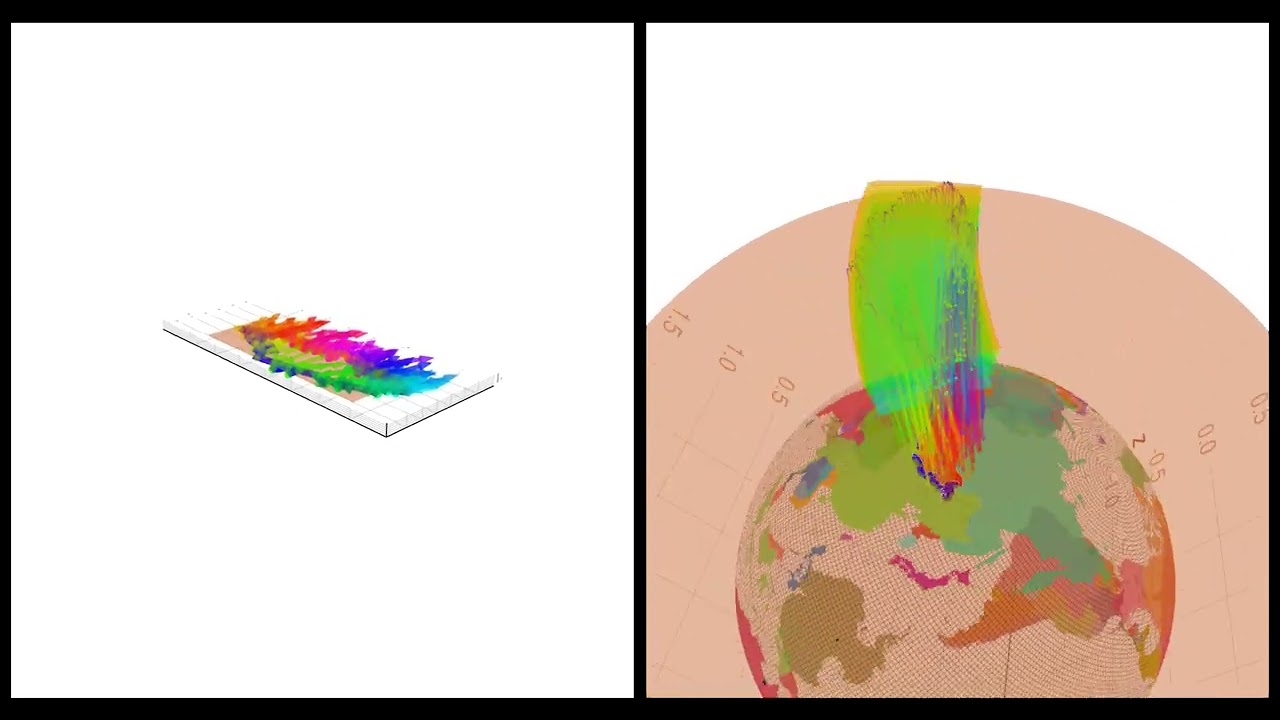
The time-evolution of a particle of unit mass falling to the Earth’s surface is derived from a function called the Hamiltonian. The Hamiltonian is defined on the phase space, where the specification of the position and momentum of the particle requires a 6-dimensional vector [q; p]. In terms of position ‘q’ and momentum ‘p’, the Hamiltonian is defined as: the squared norm of p over two, plus the norm of q times the gravitational constant ‘g’. The exterior derivative of the gravitational work 1-form (the stack) equals approximately zero (it’s constant,) because seconds after the beginning of falling to Earth, the particle’s still near the surface. So, the Hamiltonian is defined on the cotangent bundle of a 3-dimensional configuration space, which is a 6-dimensional symplectic manifold (also known as phase space.)
Under gravity, the particle falls along a geodesic curve (radial lines) in the configuration space. The value of the Hamiltonian function is constant throughout the motion, which implies the conservation of the sum of kinetic and potential energies. In the phase space, there is a 5-dimensional region containing a 4-dimensional family of the Hamiltonian flow trajectories. The reduced phase space, whose points represent these trajectories, is itself a 4-dimensional symplectic manifold. The degree’s of freedom of the 5-dimensional region can be thought of as the latitude and longitude coordinates along with a 3-vector momentum vector. However, the 4-dimensional symplectic manifold removes an axis from the momentum vector. The partial component of the momentum vector that is removed from the phase space is calculated by projecting the momentum vector on the line tangent to the trajectory. It’s remarkable that the reduced phase space can still be the configuration space of a smaller physical system and is allowed to have its own reality.