filmov
tv
Controllability, Reachability, and Eigenvalue Placement [Control Bootcamp]

Показать описание
This lecture explains the equivalence of controllability, reachability, and the ability to arbitrarily place eigenvalues of the closed loop system.
These lectures follow Chapter 8 from:
"Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz
This video was produced at the University of Washington
These lectures follow Chapter 8 from:
"Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz
This video was produced at the University of Washington
Controllability, Reachability, and Eigenvalue Placement [Control Bootcamp]
A Conceptual Approach to Controllability and Observability | State Space, Part 3
Reachability and Controllability with Cayley-Hamilton [Control Bootcamp]
Control: Pole (Eigenvalue) Placement (Lectures on Advanced Control Systems)
Reachability and observability
Stability and Eigenvalues [Control Bootcamp]
Reachability of State-space Models
Degrees of Controllability and Gramians [Control Bootcamp]
Reachability and Controllability Gramians
Discrete-Time-Systems - Reachability & Controllability (Lecture 15 - Part I)
Reachability Analysis of Pushdown Systems | Ahmed Bouajjani
Controllability
Controllability [Control Bootcamp]
Lecture 10 - Control Systems II, ETH Zurich(Spring 2018)
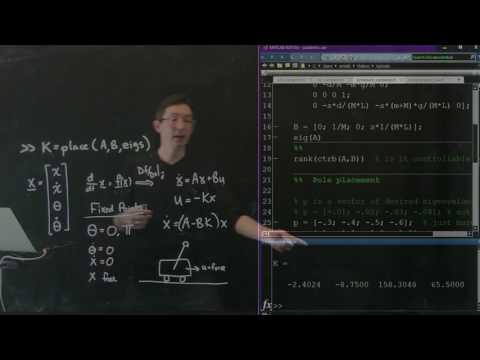
Pole Placement for the Inverted Pendulum on a Cart [Control Bootcamp]
Example 12.3 from N Nise on Pole Placement from User Requirements (g), 6/4/2016
39 Reachability same as Controllability for LTI systems
Finding the Eigenvalues of a Controllable Canonical Form State Matrix, 10/3/2016
Controllability and Reachability
Introduction to Controllability
State constrained optimal control problems via reachability approach by Athena Picarelli
l6v2 Brief intro to the definition of controllability and reachability
Lecture 9 - Control Systems II, ETH Zurich(Spring 2018)
ViveLab tutorial part 12 - Reachability test
Комментарии
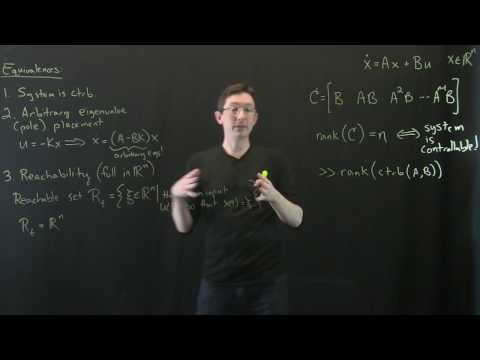 0:10:49
0:10:49
 0:13:30
0:13:30
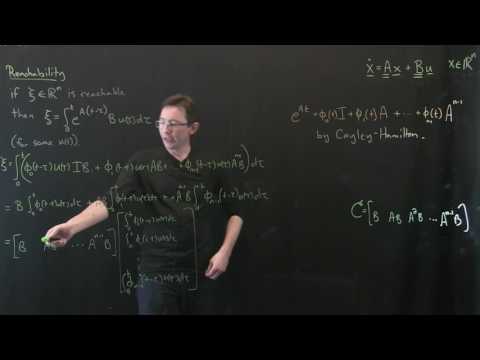 0:10:30
0:10:30
 0:12:50
0:12:50
 0:06:33
0:06:33
 0:19:30
0:19:30
 0:30:01
0:30:01
 0:15:24
0:15:24
 0:19:56
0:19:56
 0:21:43
0:21:43
 0:15:48
0:15:48
 0:10:46
0:10:46
![Controllability [Control Bootcamp]](https://i.ytimg.com/vi/u5Sv7YKAkt4/hqdefault.jpg) 0:32:30
0:32:30
 1:30:24
1:30:24
 0:12:55
0:12:55
 0:05:22
0:05:22
 0:12:14
0:12:14
 0:03:55
0:03:55
 0:50:41
0:50:41
 0:26:35
0:26:35
 0:44:36
0:44:36
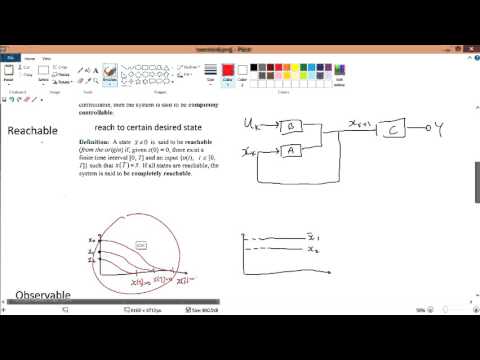 0:10:03
0:10:03
 1:29:54
1:29:54
 0:01:24
0:01:24