filmov
tv
Gaussian Elimination with Infinitely Many Solutions | Linear Algebra Exercises

Показать описание
We go over solving a system of linear equations with infinite solutions using Gaussian elimination. In doing this, we reduce the matrix to row echelon form and then perform back substitution and parameterization then solve for the leading variables to get parametric equations describing the infinite solution set. A parametric description of the solution set implies infinitely many solutions. #linearalgebra
Join Wrath of Math to get exclusive videos, music, and more:
0:00 Intro
0:10 Create Augmented Matrix
0:32 Gaussian Elimination on the Matrix
2:42 Solution Set
4:28 Conclusion
◉Textbooks I Like◉
★DONATE★
Thanks to Loke Tan, Raül Beienheimer, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!
Outro music is mine. You cannot find it anywhere, for now.
Follow Wrath of Math on...
Join Wrath of Math to get exclusive videos, music, and more:
0:00 Intro
0:10 Create Augmented Matrix
0:32 Gaussian Elimination on the Matrix
2:42 Solution Set
4:28 Conclusion
◉Textbooks I Like◉
★DONATE★
Thanks to Loke Tan, Raül Beienheimer, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!
Outro music is mine. You cannot find it anywhere, for now.
Follow Wrath of Math on...
Gaussian Elimination Method on System of Equations with Infinitely Many Solutions | Glass of Nubmers
Gaussian elimination - A case of infinitely many solutions
Gaussian Elimination with Infinitely Many Solutions | Linear Algebra Exercises
Infinitely many Solutions ( Gaussian Elimination ) Systems of equations
Solving a 3x3 system of equations using Gaussian elimination - infinitely many solutions
PreCalculus - Matrices & Matrix Applications (9 of 33) Gaussian Elimination: 3x3, Infinite Solut...
Infinitely many solutions from Gauss-Jordan elimination method
Gaussian Elimination | Infinite many solutions | Linear Algebra
Linear system with infinitely many solutions (with Gauss-Jordan elimination)
Gaussian Elimination | Infinite Solutions | Linear Algebra
Gaussian Elimination & Row Echelon Form
📚 How to use Gaussian elimination to solve a system with infinite solutions
Solving a 3x5 system of equations using Gaussian elimination - infinitely many solutions
Gaussian Elimination: Unique and Multiple solutions
Gauss Jordan (RREF) elimination for Ax=0, infinitely many solutions
Solving a 4x4 system of equations using Gaussian elimination - infinitely many solutions
Gaussian Elimination | One Solution | Linear Algebra
Solve a system of equations with infinitely many solutions using Gauss Jordan elimination.
Gaussian Elimination (4 examples)
4.18 Cases of Gaussian elimination method - Unique , No solution and Infinitly many solutions
Lec3/System of Linear Equations/Gauss Elimination if Infinitely Many Solutions Exist
Gaussian Elimination- Infinite Solutions Example
System with Infinitely Many Solutions
Gaussian elimination with infinite or no solutions
Комментарии
 0:11:09
0:11:09
 0:05:16
0:05:16
 0:05:08
0:05:08
 0:15:47
0:15:47
 0:04:16
0:04:16
 0:07:08
0:07:08
 0:03:51
0:03:51
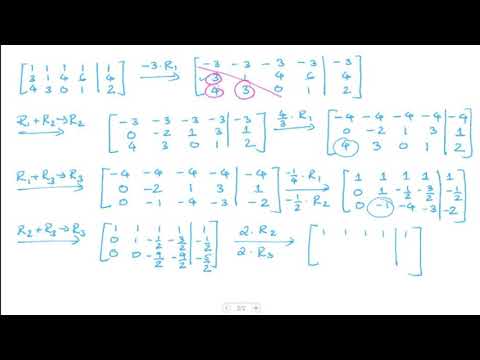 0:40:21
0:40:21
 0:10:13
0:10:13
 0:08:37
0:08:37
 0:18:40
0:18:40
 0:05:23
0:05:23
 0:07:17
0:07:17
 0:53:15
0:53:15
 0:10:45
0:10:45
 0:05:50
0:05:50
 0:08:16
0:08:16
 0:11:45
0:11:45
 0:26:07
0:26:07
 0:08:14
0:08:14
 0:26:57
0:26:57
 0:17:30
0:17:30
 0:14:47
0:14:47
 0:07:54
0:07:54