filmov
tv
6 methods of evaluating the limit of a multivariable function (calculus 3)

Показать описание
6 ways of evaluating the limit of a multivariable function that you need to know for your calculus 3 class! Subscribe to @bprpcalculusbasics for more calculus tutorials!
0:00 1. Just plug in
0:58 2. Do algebra (just like calculus 1)
3:47 3. Substitution
5:23 4. Separable (i.e. the limit of a product is the product of the limits when they both exist)
10:25 5. Polar (when (x,y) approaches (0,0))
15:46 6. Squeeze theorem
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
0:00 1. Just plug in
0:58 2. Do algebra (just like calculus 1)
3:47 3. Substitution
5:23 4. Separable (i.e. the limit of a product is the product of the limits when they both exist)
10:25 5. Polar (when (x,y) approaches (0,0))
15:46 6. Squeeze theorem
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
6 methods of evaluating the limit of a multivariable function (calculus 3)
Evaluation of Postfix Expression | Examples | Data Structures | Lec-20 | Bhanu Priya
6 Methods of evaluating limits of a function, Direct susbstitution East Academia Calculus
Intro to Evaluating Algebraic Expressions | How to Evaluate Algebraic Expressions | Math with Mr. J
Nested Scheme - Horner’s Method - Evaluating Polynomials
The reference triangle method for evaluating trigonometric functions
6. Evaluating the Performance of Machine Learning Algorithm in Python || Dr. Dhaval Maheta
Evaluating Limits By Factoring
This tool will help improve your critical thinking - Erick Wilberding
Math Antics - Order Of Operations
The determinant | Chapter 6, Essence of linear algebra
03 - Evaluating Numerical Expressions, Part 1
Evaluating limits by Conjugate Method - Limits and Radicals - Calculus
Ingenious Tricks for Evaluating the Hexic Algebraic Expression x^6+1/x^6 | Math Olympiad
Claims, Evidence, and Reasoning.
Eco-Schools Seven Steps: Step 6 - Monitoring and Evaluating
How To Calculate Square Roots - Numerals That Changed Math Forever
Evaluating Limits by Rationalization Method - Problem 6 - Limits - Diploma Engineering Mathematics 2
Algebra Basics: Solving 2-Step Equations - Math Antics
How To Use Reference Angles to Evaluate Trigonometric Functions
Bloom's Taxonomy In 5 Minutes | Blooms Taxonomy Explained | What Is Bloom's Taxonomy? | Si...
What is Critical Thinking?
3.2 Job Sequencing with Deadlines - Greedy Method
How to Evaluate Functions? Evaluating Function - General Mathematics
Комментарии
 0:24:22
0:24:22
 0:04:23
0:04:23
 0:11:49
0:11:49
 0:05:32
0:05:32
 0:06:30
0:06:30
 0:08:10
0:08:10
 0:17:24
0:17:24
 0:11:35
0:11:35
 0:05:20
0:05:20
 0:09:40
0:09:40
 0:10:03
0:10:03
 0:05:44
0:05:44
 0:16:51
0:16:51
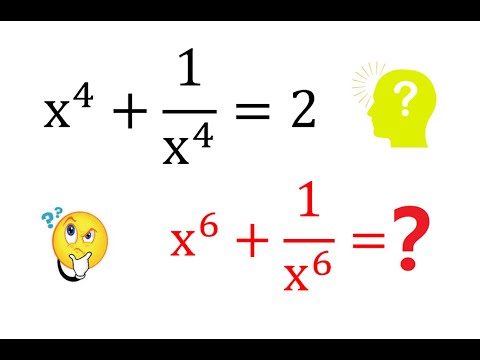 0:03:18
0:03:18
 0:02:06
0:02:06
 0:00:44
0:00:44
 0:10:16
0:10:16
 0:07:45
0:07:45
 0:10:29
0:10:29
 0:10:59
0:10:59
 0:05:17
0:05:17
 0:02:30
0:02:30
 0:13:29
0:13:29
 0:06:52
0:06:52