filmov
tv
Relativity 105d: Acceleration - Twin Paradox and Proper Time Along Curves (Rindler Metric)

Показать описание
Previous videos on the calculating the lengths of curves in Tensor Calculus series:
0:00 Intro
1:43 Proper Time review
4:09 Proper Time for non-inertial worldline
6:20 Twin Paradox Calculation
8:11 Reversed Triangle Inequality
12:03 Twin Paradox Resolved
14:39 Proper Time along Curves
18:04 Example calculation (inertial coordinates)
22:27 Example calculation (Rindler coordinates)
27:04 Proper Time Curves Conclusion
30:01 Summary
Relativity 105d: Acceleration - Twin Paradox and Proper Time Along Curves (Rindler Metric)
Relativity 105a: Acceleration - Hyperbolic Motion and Rindler Horizon
The simplest solution to Twin Paradox from special relativity (no GR, no acceleration)
Relativity 105f: Acceleration - Geodesics, Curved Light Beams (Rindler Coordinates)
Relativity 105b: Acceleration - Bell's Spaceship Paradox and Rindler Coordinates
Solving Einstein's Twin Paradox
Special Relativity moving goalposts: Minkowski
Accelerated reference frame in a spacetime diagram - Special Relativity Sandbox
Rindler Gravity (vm6502q/OpenRelativity)
Answer: Is Einstein's Rotating Time Possible? (Twins Paradox)
Rough Rindler Transform Handsketch For Back Rocket's perspective in Bells Paradox
25 General Relativity Accelerating Clocks in Special Relativity and the Twins yet again
Relativity 105e: Acceleration - Covariant Derivative in Flat Spacetime (Rindler Coordinates)
Special Relativity Lec 2 Part 3
Relativity|Causality|SpaceTime - TimeDilation (Hi-Speed/Gravity) | Length Contraction | Twin Paradox
Relativity 003 Twin Paradox 20200331 085609
Twin Paradox (without acceleration)
INTRODUCTION TO ESPECIAL RELATIVITY. Lesson 22: Transformation of acceleration.
Acceleration in Special Relativity
Relativity 105c: Acceleration - The Jacobian (changing basis in curvilinear Rindler coordinates)
Does the twin paradox break special relativity?
The Twin Paradox
SPACE TIME AND TWIN PARADOX
Critique of Don Lincoln's twin paradox video.
Комментарии
 0:32:27
0:32:27
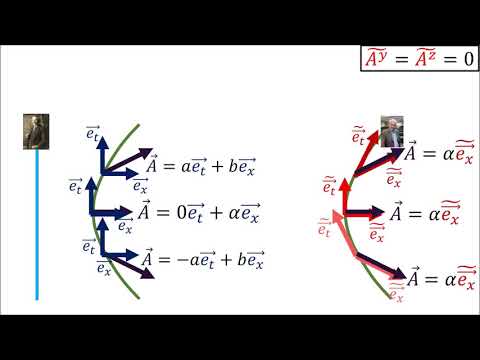 0:31:37
0:31:37
 0:02:27
0:02:27
 0:30:17
0:30:17
 0:34:22
0:34:22
 0:08:51
0:08:51
 0:16:34
0:16:34
 0:00:42
0:00:42
 0:00:56
0:00:56
 0:03:26
0:03:26
 0:00:12
0:00:12
 0:39:34
0:39:34
 0:27:17
0:27:17
 0:12:47
0:12:47
 0:01:00
0:01:00
 0:03:52
0:03:52
 0:03:32
0:03:32
 0:14:45
0:14:45
 0:10:18
0:10:18
 0:34:45
0:34:45
 0:24:53
0:24:53
 0:48:44
0:48:44
 0:24:30
0:24:30
 0:13:18
0:13:18