filmov
tv
The million dollar equation (Navier-Stokes equations)

Показать описание
PLEASE READ PINNED COMMENT
In this video, I introduce the Navier-Stokes equations and talk a little bit about its chaotic behavior. Make sure to like and subscribe!
Follow me!
In this video, I introduce the Navier-Stokes equations and talk a little bit about its chaotic behavior. Make sure to like and subscribe!
Follow me!
The million dollar equation (Navier-Stokes equations)
Navier Stokes Equation | A Million-Dollar Question in Fluid Mechanics
Navier-Stokes Equations - Numberphile
The Navier-Stokes Equations in your coffee #science
The Trillion Dollar Equation
This $1,000,000 Problem Can Revolutionize Weather Modeling - Navier-Stokes Existence and Smoothness
Millennium Maths Problems Explained in 90 Seconds
Navier Stokes equation
Millennium Problems: Math’s Million Dollar Bounties
The million dollar problem of fluid dynamics - Navier Stokes existence and smoothness
The Navier-Stokes Equations in 30 Seconds | Incompressible Fluid Flow
The Man Who Solved the $1 Million Math Problem...Then Disappeared
Do you want a million dollar? Solve Navier-Stokes' equation.
The Million-Dollar Maths Equations
The Million Dollar Equations - with Tom Crawford
Introduction to the Navier-Stokes Equations
Description and Derivation of the Navier-Stokes Equations
Navier-Stokes Equation Final Exam Question
Navier-Stokes Final Exam Question (Liquid Film)
Little girl solved millennium Maths problem 🔥.
A Brief History of the Navier-Stokes Equations
Take the Navier-Stokes equations one term at a time for CFD
Turbulence and the Navier-Stokes Equations
Navier-Stokes Equations | Lecture 1 | Flow Around a Cylinder
Комментарии
 0:08:03
0:08:03
 0:07:07
0:07:07
 0:21:03
0:21:03
 0:01:00
0:01:00
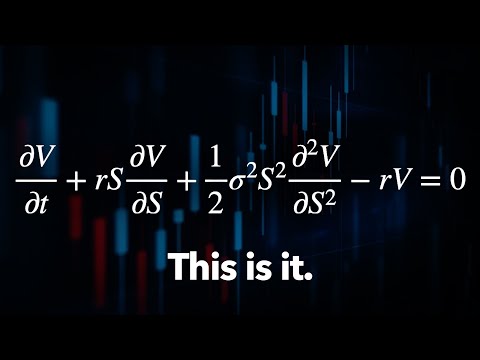 0:31:22
0:31:22
 0:08:14
0:08:14
 0:01:53
0:01:53
 0:00:16
0:00:16
 0:15:05
0:15:05
 0:01:56
0:01:56
 0:00:35
0:00:35
 0:10:45
0:10:45
 0:00:16
0:00:16
 0:13:52
0:13:52
 1:11:40
1:11:40
 0:10:02
0:10:02
 0:11:18
0:11:18
 0:14:55
0:14:55
 0:12:40
0:12:40
 0:04:28
0:04:28
 0:06:31
0:06:31
 0:00:41
0:00:41
 0:02:43
0:02:43
 0:08:47
0:08:47