filmov
tv
Maximum flow Minimum Cut Algorithm

Показать описание
There are videos for:
Queensland: General Mathematics
Queensland: Mathematical Methods
Queensland: Mathematics Specialist
Western Australia: Mathematics Applications
Western Australia: Mathematics Methods
Western Australia: Mathematics Specialist
Network Flows: Max-Flow Min-Cut Theorem (& Ford-Fulkerson Algorithm)
Maximum flow Minimum Cut Algorithm
9 Flow Maximum Flow Minimum cut
The Maximum Flow Minimum cut Theorem
Finding maximum flow through a network
Ford-Fulkerson in 5 minutes
7 Flow Maximum Flow Minimum cut
8 Flow Maximum Flow Minimum cut
Minimum cuts and maximum flow rate
Maximum Flow and Minimum Cut of a Network
9.3 Maximum flow, minimum cut
The Maximum Flow Minimum cut Theorem: Part 2
4 Flow Maximum Flow Minimum cut
Max Flow Ford Fulkerson | Network Flow | Graph Theory
Maximum flow problem - Ford Fulkerson algorithm
13. Incremental Improvement: Max Flow, Min Cut
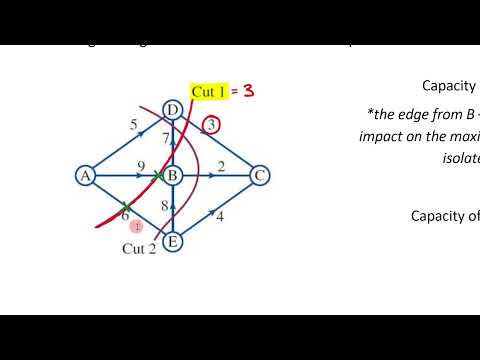
How to locate the minimum cut that represents the maximum flow capacity in a network graph
Ford Fulkerson Algorithm for Maximum Flow Problem
MAXIMAL FLOW PROBLEM | OPERATIONS RESEARCH
Max Flow, Min Cut Theorem for Flow Networks
Max-Flow Min-Cut Theorem
How to use the maximum-flow minimum-cut theorem to find the flow capacity of a network (example 1)
Flows and Cuts - Georgia Tech - Computability, Complexity, Theory: Algorithms
Proof of Max-Flow Min-Cut Theorem and Ford Fulkerson Correctness
Комментарии
 0:21:56
0:21:56
 0:14:02
0:14:02
 0:02:24
0:02:24
 0:10:17
0:10:17
 0:04:59
0:04:59
 0:05:15
0:05:15
 0:03:08
0:03:08
 0:03:31
0:03:31
 0:10:00
0:10:00
 0:07:53
0:07:53
 0:26:04
0:26:04
 0:10:48
0:10:48
 0:02:36
0:02:36
 0:13:25
0:13:25
 0:05:11
0:05:11
 1:22:58
1:22:58
 0:04:03
0:04:03
 0:09:05
0:09:05
 0:05:45
0:05:45
 0:15:19
0:15:19
 0:05:54
0:05:54
 0:04:46
0:04:46
 0:01:49
0:01:49
 0:08:11
0:08:11