filmov
tv
Example of Group Isomorphism

Показать описание
Abstract Algebra: An abelian group G has order p^2, where p is a prime number. Show that G is isomorphic to either a cyclic group of order p^2 or a product of cyclic groups of order p. We emphasize that the isomorphic property usually requires construction of an isomorphism.
Example of Group Isomorphism
Isomorphisms (Abstract Algebra)
Lots of group isomorphism examples.
GROUP ISOMORPHISM WITH EXAMPLE PROBLEM | GROUP ISOMORPHISM | EXAMPLE PROBLEM ON GROUP ISOMORPHISM |
Group Homomorphism and Isomorphism
Isomorphic Groups and Isomorphisms in Group Theory | Abstract Algebra
Abstract Algebra | Group Isomorphisms
ISOMORPHISM (DEFINITION AND EXAMPLE)- GROUP THEORY
Group Theory | Isomorphism | Examples of Isomorphism
Group Theory L6V5: An Example of Group Isomorphism
Group Isomorphism | Isomorphic Group example | Group Theory || Lecture 33
#90: Examples of group isomorphism - I
Abstract Algebra 50: An example isomorphism
Chapter 6: Homomorphism and (first) isomorphism theorem | Essence of Group Theory
Abstract Algebra 6.3: More Isomorphism Examples
Group Theory 44, Group homomorphism, Isomorphism, examples
Group Isomorphism | Isomorphism Example | Isomorphism between S3 and D3 | Group theory | Lecture 7
Binary Operations and Group Isomorphism
Abstract Algebra 6.2: Definition of Group Isomorphism
Visual Group Theory, Lecture 4.5: The isomorphism theorems
The Kernel of a Group Homomorphism – Abstract Algebra
GROUP ISOMORPHISM WITH ANOTHER EXAMPLE PROBLEM | GROUP ISOMORPHISM | GROUP THEORY | ISOMORPHISM |
Isomorphism in Group Theory with examples
GROUP ISOMORPHISM | ISOMORPHISM IN GROUP THEORY | ISOMORPHISM BETWEEN GROUPS | GROUP THEORY | DMS |
Комментарии
 0:08:33
0:08:33
 0:05:04
0:05:04
 1:03:28
1:03:28
 0:12:06
0:12:06
 0:06:03
0:06:03
 0:13:58
0:13:58
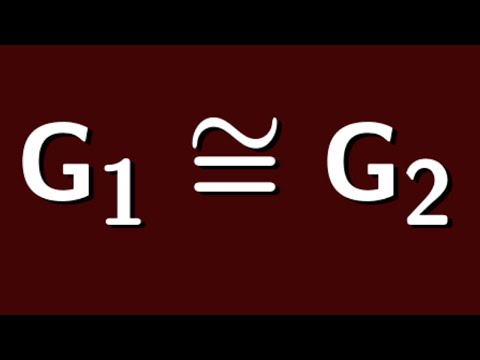 0:12:46
0:12:46
 0:13:14
0:13:14
 0:17:58
0:17:58
 0:22:58
0:22:58
 0:17:37
0:17:37
 0:09:28
0:09:28
 0:07:27
0:07:27
 0:12:47
0:12:47
 0:05:05
0:05:05
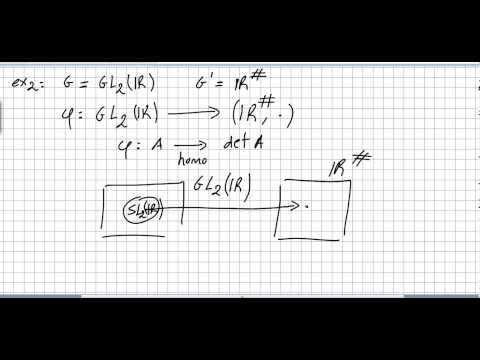 0:20:28
0:20:28
 0:08:37
0:08:37
 0:07:13
0:07:13
 0:07:03
0:07:03
 0:46:19
0:46:19
 0:04:53
0:04:53
 0:15:38
0:15:38
 0:15:06
0:15:06
 0:09:57
0:09:57