The Infinite Money Paradox

Not a real offer. Deciding whether to play a game is usually very easy… you crunch the numbers and if they work in your favor, you play. If they don’t, you shouldn’t. Mathematical case closed.

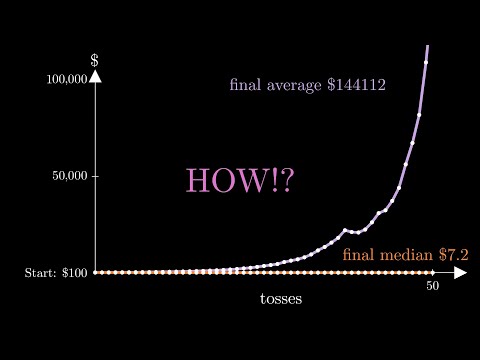
But what happens when the math of a game tells you that you have access to infinite wealth and unlimited expected value and real life tells you not to play? Enter: The St. Petersburg Paradox.

The Bernoulli family first started corresponding about the paradox in the early 1700s with a series of letters examining the puzzling math behind the simple game. But it wasn’t until 1738 when Daniel Bernoulli realized that he could factor real life utility -- how much something actually means to you -- into the calculations.

The St. Petersburg Paradox opens up doors to how we think about what math really means to us, including modern research into Prospect Theory and everyday issues like whether we decide to buy life insurance. And in the end, one thing we know for sure: we’re all much, much more than numbers.

*** SOURCES ***



*** LINKS ***

Vsauce2 Links

Hosted and Produced by Kevin Lieber

Research And Writing by Matthew Tabor

Huge Thanks To Paula Lieber

Get Vsauce's favorite science and math toys delivered to your door!

#education #vsauce2

[Lorenzo-tmcr]

Tried this a few times with my 2 euros coin. I gained 2, 2, 2, 8, 8, 16, 16, 128 and then lost my coin between the sofa cushions. So this game actually made me lose 2 euros without any reward.

[Keyboardkat]

If I had a nickel for every time that i had a nickel, i'd have a lot of nickels

[reedphillips]

“This game can’t exist!”

*MrBeast enters the room*

[Byran-opsf]

“if things go really well, things go really well”
*every 60 seconds in africa, a minute passes*

[billmcneal]

so this is where mr beast gets his money from

[jamesdickson]

see yall in 6 years when this is in everyone's recommended

[GRLDT]

"Who would empty their bank account to play a game whe-"

**Mr. Beast wants to know your location**

[mr.waffles]

“1 piece of something is called an item, 64 items is called a stack”

[SergioEduP]

Kevin: "what is a chance of infinite wealth worth for you?"

Me: Idk, like 5$ maybe

[orealis]

"...And a person with $2 should spend $3.35..."

*stonks*

[chefizzy]

Knowing my luck I’d be the only person to win $0

[Kazperian]

Vsauce makes everything interesting...

Vsauce2 makes everything mathematical

[byrontenorio]

Editing this comment 'cause I sound edgy here lmao

[duchi]

*"This game can't even exist"*
I want 10 minutes of my life back

[DavidPysnik]

The issue here is that you literally need to play the game an infinite amount of times for the infinite expected value to be valid, and that isn't possible. The better way to think of it is that the expected value can become as large as you want as long as you are willing to play a sufficiently high number of times. The question of what is good to pay is then tied to how many times you will play. It's intuitive not to pay too much to play because you know you are probably not going to get a long string of "fact" flips unless you play a ridiculous amount of times, and you know you aren't going to play a ridiculous amount of times. There is really no paradox here, so I will go back to being a logarithmic function now.

[guillis]

I’d pay one dollar, lose at the first round, and then play again with one of my 2 dollars. Bam, broke the system, I don’t need infinite luck

[epic_gamerXD]

but when u gonna talk about infinite water sources

[adamtaurus]

"If things go really well, things go really well"
Ah yes, the floor here is made of floor

[natekoyle]

Always love your videos. I always finish them with a feeling that lays somewhere in the middle of smarter/more empowered and completely dumbfounded about everything I’ve known. Which is for some reason why I love your content! Thanks Vsauce!

[Airwolf-lmcm]

Tell me if I’m missing something but the problem is that the expected value of an potentially infinite game gives no useful information. There is no paradox here. You can still pretty easily calculate that the chance of winning something is very small.
You chance to win more than 8$ is about 6%. If you are hoping for 128 that is already less than 1%.