filmov
tv
2#DeMoivresTheorem7Marks #Showthat (1 + i)^n + (1 - i)^n = 2^[(n + 2)/2] Cos (nπ/4)
Показать описание
Senior Inter Maths2A DeMoivre's Theorem LAQ 7 Marks With Complete Solutions
#aimsdtsshorts
#aimsdaretosuccess
Show that (1 + i)^2n + (1 - i)^2n = 2^(n + 1)Cos (nπ/2)
Show that (1 + i)^n + (1 - i)^n = 2^[(n + 2)/2] Cos (nπ/4)
Show that (p + i q)^ 1/n - (p + i q)^ 1/n = 2 [(p^2 + q^2)^(1/2n)] Cos [(1/n)Tan^-1(q/p)]
If α, β are the roots of x^2 - 2x + 4 = 0 then show that α^n + β^n = 2^(n+1) Cos(nπ/3)
Show that (1 + Cos β + i Sin β)^n + (1 + Cos β - i Sin β)^n = 2^(n+1) Cos^n(β/2) Cos(nβ/2)
If Cos A + Cos B + Cos C = 0 = Sin A + Sin B + Sin C then show that Cos^2(A) + Cos^2(B) + Cos^2(C) = 3/2 = Sin^2(A) + Sin^2(B) + Sin^2(C)
If n is an integer and Z = CiS β then show that [Z^(2n) - 1] / [Z^(2n) + 1] = i Tan(nβ)
If Cos A + Cos B + Cos C = 0,
Sin A + Sin B + Sin C = 0 then show that
Cos 3A + Cos 3B + Cos 3C = 3Cos (A + B + C),
Sin 3A + Sin 3B + Sin 3C = 3Sin (A + B + C),
Cos (A + B) + Cos (B + C) + Cos (C + A) = 0
If x = Cos α + i Sin α,
y = Cos β + i Sin β then show that x^m y^n + 1 / x^m y^n = 2 Cos (mα + nβ), x^m y^n - 1 / x^m y^n = 2i Sin (mα + nβ)
Show that [1 + Sin (π/8) + i Cos (π/8) by 1 + Sin (π/8) - i Cos (π/8) ]^ (8/3) = -1
#aimsdtsshorts
#aimsdaretosuccess
Show that (1 + i)^2n + (1 - i)^2n = 2^(n + 1)Cos (nπ/2)
Show that (1 + i)^n + (1 - i)^n = 2^[(n + 2)/2] Cos (nπ/4)
Show that (p + i q)^ 1/n - (p + i q)^ 1/n = 2 [(p^2 + q^2)^(1/2n)] Cos [(1/n)Tan^-1(q/p)]
If α, β are the roots of x^2 - 2x + 4 = 0 then show that α^n + β^n = 2^(n+1) Cos(nπ/3)
Show that (1 + Cos β + i Sin β)^n + (1 + Cos β - i Sin β)^n = 2^(n+1) Cos^n(β/2) Cos(nβ/2)
If Cos A + Cos B + Cos C = 0 = Sin A + Sin B + Sin C then show that Cos^2(A) + Cos^2(B) + Cos^2(C) = 3/2 = Sin^2(A) + Sin^2(B) + Sin^2(C)
If n is an integer and Z = CiS β then show that [Z^(2n) - 1] / [Z^(2n) + 1] = i Tan(nβ)
If Cos A + Cos B + Cos C = 0,
Sin A + Sin B + Sin C = 0 then show that
Cos 3A + Cos 3B + Cos 3C = 3Cos (A + B + C),
Sin 3A + Sin 3B + Sin 3C = 3Sin (A + B + C),
Cos (A + B) + Cos (B + C) + Cos (C + A) = 0
If x = Cos α + i Sin α,
y = Cos β + i Sin β then show that x^m y^n + 1 / x^m y^n = 2 Cos (mα + nβ), x^m y^n - 1 / x^m y^n = 2i Sin (mα + nβ)
Show that [1 + Sin (π/8) + i Cos (π/8) by 1 + Sin (π/8) - i Cos (π/8) ]^ (8/3) = -1
0:08:15
2#DeMoivresTheorem7Marks #Showthat (1 + i)^n + (1 - i)^n = 2^[(n + 2)/2] Cos (nπ/4)
0:09:59
1#DeMoivresTheorem7Marks #Showthat (1 + i)^2n + (1 - i)^2n = 2^(n + 1)Cos (nπ/2)
0:11:21
28) Show that (1+i)^2n +(1-i)^2n = 2^n+1 Cos nπ/2 || Demoivre's Theorem || 7 Marks Problem
0:07:01
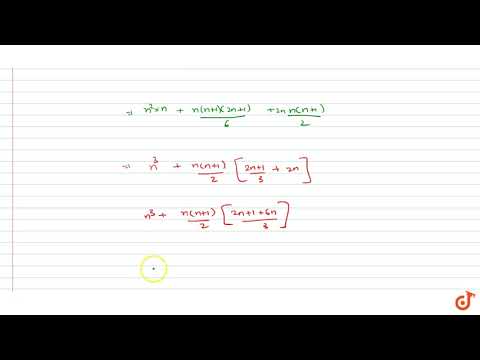
If n is a positive integer, show that, `(n+1)^(2) + (n+2)^(2) + …+ 4n^(2) = (n)/(6)(2n+1)(7n+1)`
0:03:02
If `n` is a positive integer show that `(n+1)^2+(n+2)^2+....4n^2=n/6(2n+1)(7n+1)`
0:06:22
If n is any integer then show that (1 + i)²ⁿ + (1 – i)²ⁿ 2ⁿ+¹ Cos(n pi / 2) @EAG
0:13:14
show that (P+ⅈQ)^(1/n)+(P-ⅈQ)^(1/n)=2(P^2+Q^2 )^(1/2n)⋅cos[1/n〖tan〗^(-1)〖Q/P〗 ] and (x-1)^n=x^n...
0:12:32
If n is an integer then show that(1+i)^2n + (1-i)^2n=2^(n+1) cos n pi /2
0:11:27
5#DeMoivresTheorem (1 + Cos β + i Sin β)^n + (1 + Cos β - i Sin β)^n = 2^(n+1)Cos^n(β/2)Cos(nβ/2)...
0:08:32
If n is a positive integer show that (1+I)^2n + ( 1-i)^2n = 2^(n+1/2) cos n pi /2
0:26:18
problems on De-Moivre's Theorem | solved examples |TS AP senior Inter mathematics 2A |complex n...
0:02:53
C(n,0) - C(n,2) + C(n,4) - ....... = `2^(n/2) cos( n pi/4)`
0:05:22
9#DeMoivre'sTheoren If x=Cosα+iSinα, y=Cosβ+iSinβ ThenShowThat x^m y^n + 1 /x^m y^n = 2Cos (mα ...
0:05:57
(1+ i)^2n + (1-i)^2n = 2^n+1 Cos(n pi /2) ; De-Movire's theorem@EAG
0:09:13
If n is a positive integer show that (1+I)^n + ( 1-i)^n = 2^(n+2)/2 cos n pi /4
0:07:17
If n ,showthat(1+costhet+isintheta)^n+(1+costheta -isin theta)^n=2^(n+1)cos^n(theta/2)cos(ntheta/2)
0:05:45
Z = Cis (theta) then Z^(2n) - 1 / Z^(2n) + 1 = i tan n(theta)@EAG
0:04:20
What is the smallest positive integer n for which (1+i)^2n=(1-i)^2n .....?
0:09:01
Show that one value of [(1+sin〖π/8〗+ⅈ cos〖π/8〗)/(1+sin〖π/8〗-ⅈ cos〖π/8〗 )]^(8/3) ⅈs-1 #iit jee...
0:04:08
Complex numbers- problem if x+iy = 1/(1+cos theta + i sin theta) then show that 4x^2=1
0:06:39
7#DeMoivre's Theorem If Z = CiS θ then show that [Z^(2n) - 1] / [Z^(2n) + 1] = i Tan(nθ)
0:25:03
De-moivre's theorem complex numbers| (Z^2n -1)/(Z^2n +1) = i tan(n*theta)|TS AP INTER mathemati...
0:03:23
If `(1+x)^n=a_0+a_1x+a_2x^2+....+a_nx^n`, then
0:02:19
If `x=a+b,y=aomega+bomega^2, z=aomega^2+bomega`, prove that `x^3+y^3+z^3=3(a^3+b^3)`
Комментарии