The Random Walk Model

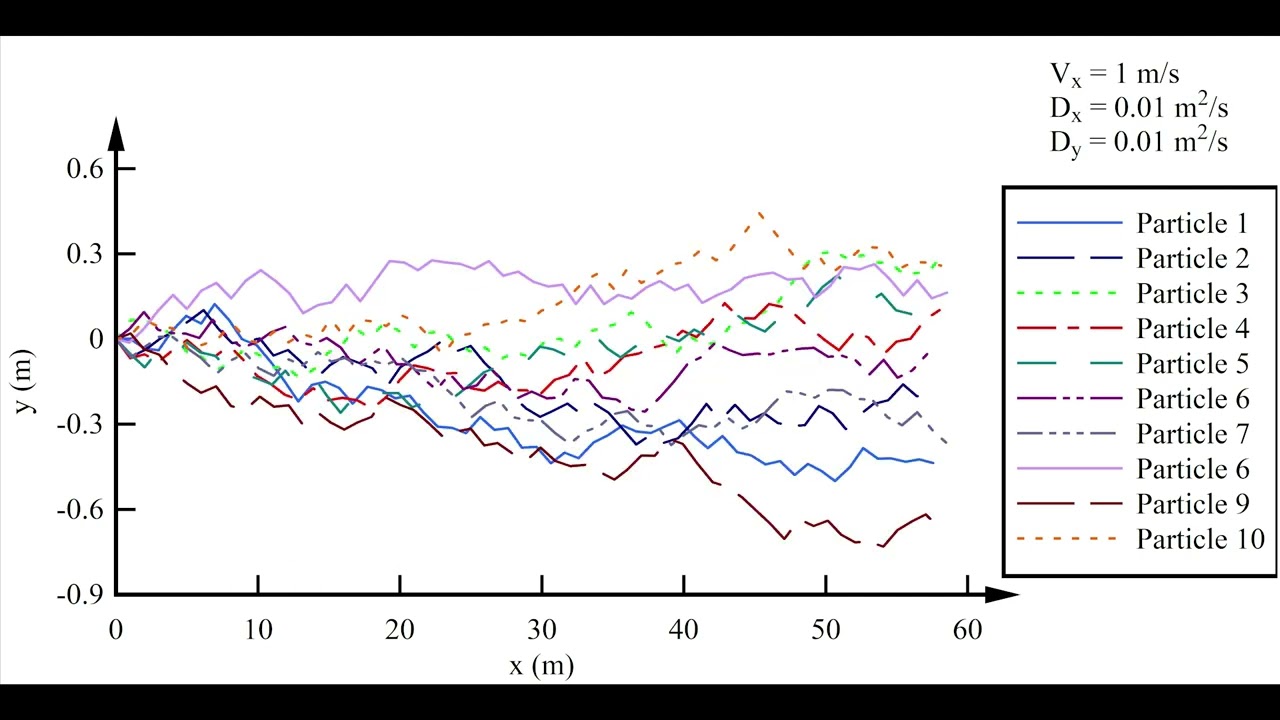
In turbulent flows, the chaotic motion of fluid and contaminant particles may be modelled by the ‘random walk’ (Chanson 2004b, pp. 93-95). The random walk model assumes that each particle is advected by the main current and displaced longitudinally, vertically and laterally by turbulent structures. With increasing time, the particles become separated further and further by the random chaotic motion.
The random walk model simulates discrete mixing at a series of time steps, and each step is un-correlated to the previous one assuming a homogeneous and stationary turbulence. For long diffusion times and a large number of particles, the random walk model yields a standard normal (Gaussian) distribution.
A related model is Langevin’s model of turbulent dispersion (Pope 2000, pp. 501-502; Chanson 2004b, p. 95). Shortly after Albert Einstein (1879-1955) identified Brownian motion, Paul Langevin (1872-1946) formulated a theory to model the velocity of a particle undergoing Brownian motion. Langevin's approach had great utility in describing molecular fluctuations in other systems, including non-equilibrium thermodynamics.
The random walk model is a fundamental concept for the transport of contaminants in turbulent flows. These are discussed in the relevant Youtube video movies in the same Playlist at:

Advanced hydraulics of open channel flows [Playlist]
Fundamentals of open channel hydraulics [Playlist]
Environmental hydraulics of open channel flows [Playlist]
Applied Hydrodynamics [Playlist]

Laminar and turbulent flows
Turbulence

References
POPE, S.B. (2000). "Turbulent Flows." Cambridge University Press, 771 pages.
CHANSON, H. (2004a). "The Hydraulics of Open Channel Flow: An Introduction." Butterworth-Heinemann, 2nd edition, Oxford, UK, 630 pages (ISBN 978 0 7506 5978 9).
CHANSON, H. (2004b). "Environmental Hydraulics of Open Channel Flows." Elsevier-Butterworth-Heinemann, Oxford, UK, 483 pages (ISBN 978 0 7506 6165 2).
CHANSON, H. (2014). "Applied Hydrodynamics: An Introduction." CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 448 pages & 21 video movies (ISBN 978-1-138-00093-3).