Infinite gift and the painter’s #paradox

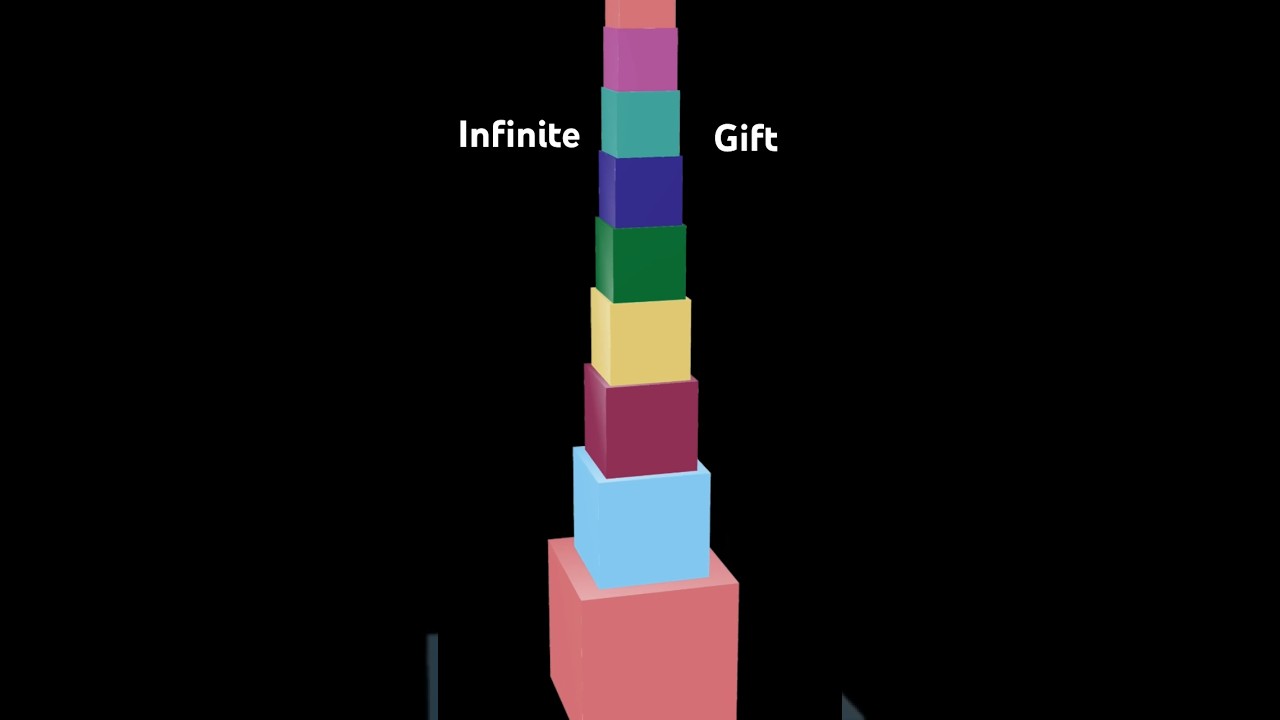
In this animation, we show an approximation of the mathematical object colloquially referred to as the "infinite gift." This gift is somewhat paradoxical in nature because it is infinitely long and requires an infinite amount of wrapping paper to cover, yet it only encloses a finite area. This object is a discrete analog of the more famous "Gabriel's horn," which is an object studied in most integral calculus classes as it is an object enclosing finite volume but has an infinite surface area.

One major purpose of this video is to investigate the different, but related, infinite sums of 1/n and 1/sqrt(n cubed). These sums both have interpretations in terms of the infinite gift, and one of them diverges while the other converges.

Thanks!

Here is a slower, wide format, high definition alternate version of this video:

#manim #infinitegift #paintersparadox #gabrielshorn #harmonicseries #infiniteseries #convergence #divergence

To learn more about animating with manim, check out:

[JordHaj]

The stack's height is infinite, visible surface area is infinite, but the volume is finite. Math is fascinating

[jk-njyo]

And thinking about how they would all fit inside of each other

[EvilDudeLOL]

"It's a cake you can eat, but not frost."
-Vsauce

[davidgillies]

Volume is zeta(1.5) in case anyone was wondering.

[mehdimabed]

The painter's paradiox is one of my favorite and fascinantes me the most ! I can't handle how the surface isn't "contained" in the volume... Cool visualization !

[SirNobleIZH]

someone needs. to make a satisfying render of these cubes with open tops falling into each other

[PiranhaFlip]

Was about to write a comment about the area equation missing an additional area that is left uncovered by each successive cube (would just be (1/(root1))^2 which is just 1, as it would just be the view from above at infinity) but then remembered the series diverges so it's a moot point anyway. Great video!

[The_True_J]

I heard a great solution to the painters paradox. It was that it's trying to combine 2 units that are inherently different. Surface area is not volume. It's like asking how many meters are in 1 liter of water. Because we all know that paint has a thickness, but when we look at a wall, it doesn't feel like the paint has thickness, the painters' paradox persists.

[peterboneg]

I think you could paint it if the thickness of paint you use decreases. That's basically what happens when you fill the volume with paint, the thickness of paint is reducing.

[wyboo]

the volume is actually Zeta(3/2) where Zeta is the Riemann Zeta function. also reminds me of Gabriel's Horn

[TimJSwan]

Sir, we have enough paint to fill the entirety of your home, but definitely not enough to paint your infinite walls.

[Rafael-pimd]

Imagining you're inside this structure, you'd see the volume shrinking til it becomes a Zero Dimension point. Outside of it you can see the surface approaching a 1D line

[silhouetta]

I love when these are something I actually know. I was able to pause and figure out the convergence/divergence before you said it! Makes me feel like a total genius 😅

[Discovery.specimen]

I want to be a mathematician and physicist. I love you bro ❤️ u help me to understand from the core

[robbierobinson]

This is an example of the answer to a great riddle.

[arthurau]

Is this like a 3D version of how the perimeter of an island can technically go to infinity as you decrease the minimum measurement length, but the area remains finite?

[robdom]

- Have you started your homework yet?
- Almost! I just gotta stack these boxes first...

[tylosenpai]

Integraling the Volume gives a fraction, but when variable is a polynomial of n >= -1, it soars (When it's 1/x, you just get ln x, which diverges with higher x)

[NStripleseven]

That’s a weird concept. You can’t paint the outside because it has infinite area, but you can paint the inside because it has finite volume.

[powertomato]

Has some fractal vibes to it. A Koch curve has an infinite length, but a finite area, if you create an object by rotating the curve, it would also have infinite area and finite volume