filmov
tv
A Golden Equation #algebra

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #counting #geometry #numbertheory #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #counting #geometry #numbertheory #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Golden Equation #algebra
Solving A Golden Equation #algebra
The Golden rule of Algebra - Do the same thing on both sides
Golden Ratio | What is the Value of the Algebraic Expression? | Conjugate | Math Olympiad
'Golden Equations: Unlocking Olympic Algebra'
Golden Proof - Numberphile
Solving A Golden Logarithm #algebra
A Golden Olympiad Algebra Equation Problem | 2 Methods - use Inequality and ...
Continuity & Differentiability in 10 Mins🔥😱| Rapid Revision Class 12 Maths | Board Exams 2025...
A Golden Exponential Equation #maths #algebra #exponential
The golden rule - how to solve basic algebraic equations - lesson 1.2
Golden Ratio & How It Is Calculated : Math & Algebra
Golden Rules of Algebra
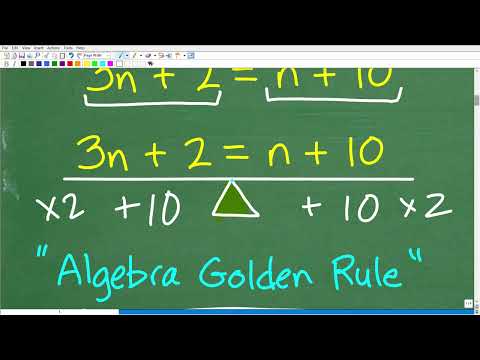
3n + 2 = n + 10, follow the “Golden Rule of Algebra”
Golden Rule in Algebra
Can You Outsmart This Algebra Challenge? | The Golden Ratio
'Wonderful Equations: Cracking Olympic Algebra'
Mathematics - Fibonacci Sequence and the Golden Ratio
Golden Maths Series Algebra | Best Book For Algebra | #Algebra
A Golden Answer
REMEMBER the Golden Rule of #Algebra! #Shorts #SAT
Japanese Math Olympiad Problem #shorts #maths #mathematics #olympiad #algebra
LT8D2 Practicing the Golden Rule of Algebra
A Nice Algebraic Equation ....|| A Golden Olympiad Exponential Problem....||| #math903
Комментарии
 0:06:11
0:06:11
 0:08:50
0:08:50
 0:04:05
0:04:05
 0:04:05
0:04:05
 0:03:05
0:03:05
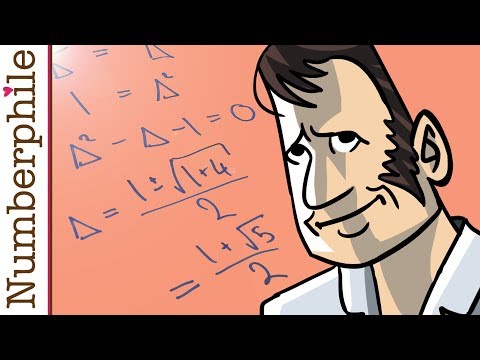 0:04:56
0:04:56
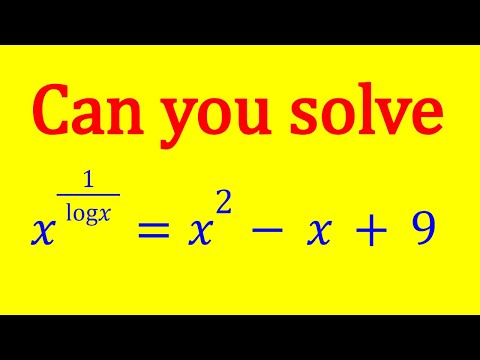 0:08:28
0:08:28
 0:14:23
0:14:23
 0:08:04
0:08:04
 0:00:51
0:00:51
 0:03:08
0:03:08
 0:01:34
0:01:34
 0:03:24
0:03:24
 0:14:08
0:14:08
 0:00:16
0:00:16
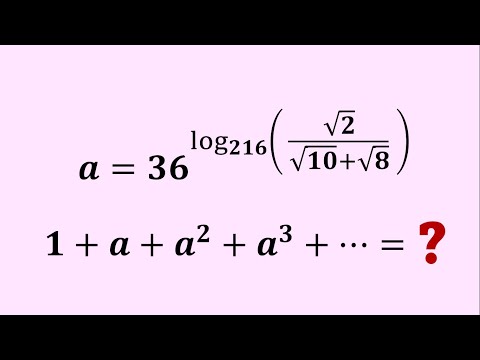 0:11:02
0:11:02
 0:06:54
0:06:54
 0:24:54
0:24:54
 0:00:38
0:00:38
 0:03:15
0:03:15
 0:00:29
0:00:29
 0:00:06
0:00:06
 0:09:08
0:09:08
 0:03:19
0:03:19