Caroline Turnage-Butterbaugh – Gaps between zeros of the Riemann zeta-function

This is the 5/5/21 talk given by Caroline Turnage-Butterbaugh for the Vanderbilt number theory seminar.
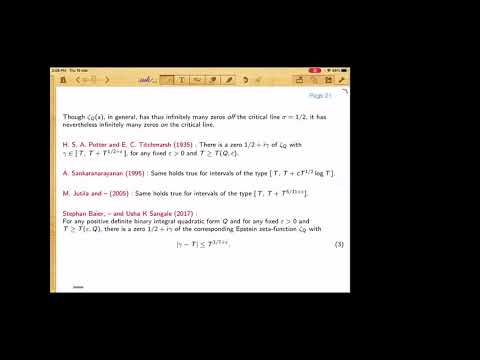
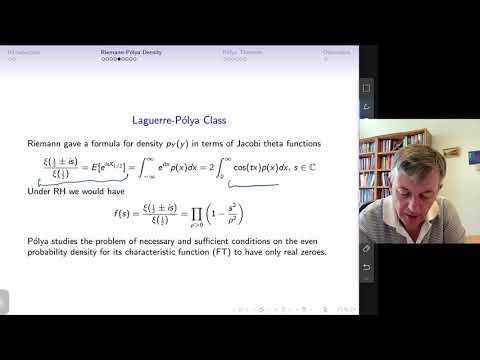
Abstract: Let 𝛾1≤𝛾2≤⋯ denote the ordinates of the complex zeros of the Riemann zeta-function function in the upper half-plane. The average distance between 𝛾𝑛 and 𝛾𝑛+1 is 2𝜋/log𝛾𝑛 as 𝑛→∞. An important goal is to prove unconditionally that these distances between consecutive zeros can much, much smaller than the average for a positive proportion of zeros. We will discuss the motivation behind this endeavor, progress made assuming the Riemann Hypothesis, and recent work with A. Simonič and T. Trudgian to obtain an unconditional result that holds for a positive proportion of zeros.