Linear Regression - Fun and Easy Machine Learning

Linear regression and just how simple it is to set one up to provide valuable information on the relationships between variables. Watch this video for a quick and easy solution to do a linear regression in Excel.

Want to learn more?

Hi and welcome to a new lecture in the Fun and Easy Machine Learning Series. Today I’ll be talking about Linear Regression. We show you also how implement a linear regression in excel.

Linear regression attempts to model the relationship between two variables by fitting a linear equation to observed data. One variable is considered to be an explanatory variable, and the other is considered to be a dependent variable.

Dependent Variable – Variable who’s values we want to explain or forecast
Independent or explanatory Variable that Explains the other variable. Values are independent.

Dependent variable can be denoted as y, so imagine a child always asking y is he dependent on his parents.
And then you can imagine the X as your ex boyfriend/girlfriend who is independent because they don’t need or depend on you. A good way to remember it. Anyways

Used for 2 Applications
To Establish if there is a relation between 2 variables or see if there is statistically signification relationship between the two variables-

• To see how increase in sin tax has an effect on how many cigarettes packs are consumed
• Sleep hours vs test scores
• Experience vs Salary
• Pokemon vs Urban Density
• House floor area vs House price
Forecast new observations – Can use what we know to forecast unobserved values
Here are some other examples of ways that linear regression can be applied.

• So say the sales of ROI of Fidget spinners over time.
• Stock price over time
• Predict price of Bitcoin over time.
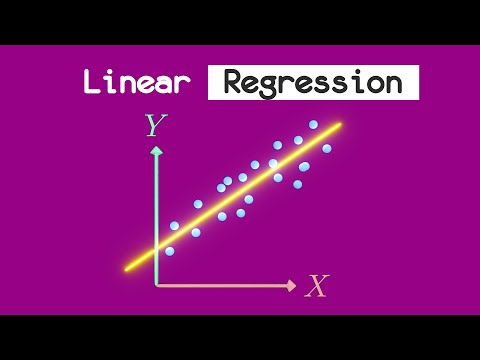
Linear Regression is also known as the line of best fit

The line of best fit can be represented by the linear equation y = a + bx or y = mx + b or y = b0+b1x
You most likely learnt this in school.

So b is is the intercept, if you increase this variable, your intercept moves up or down along the y axis.
M is your slope or gradient, if you change this, then your line rotates along the intercept.

Data is actually a series of x and y observations as shown on this scatter plot. They do not follow a straight line however they do follow a linear pattern hence the term linear regression
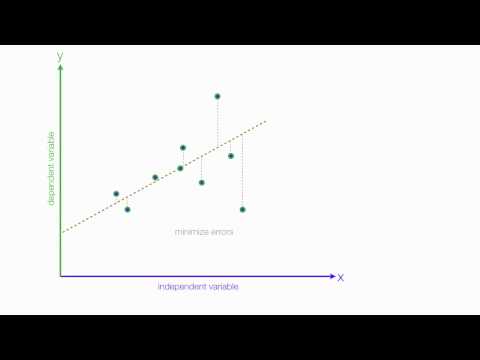
Assuming we already have the best fit line, We can calculate the error term Epsilon. Also known as the Residual. And this is the term that we would like to minimize along all the points in the data series.
So say if we have our linear equation but also represented in statistical notation. The residual fit in to our equation as shown y = b0+b1x + e

------------------------------------------------------------
Support us on Patreon
Chat to us on Discord
Interact with us on Facebook
Check my latest work on Instagram
Learn Advanced Tutorials on Udemy
------------------------------------------------------------
To learn more on Artificial Intelligence, Augmented Reality IoT, Deep Learning FPGAs, Arduinos, PCB Design and Image Processing then check out

Please Like and Subscribe for more videos :)

[zeal]

That ex girlfriend concept hurt bro!!😂

[blushingbutterfly]

"think of x as your ex-girlfriend because they are independant and dont need you"

why must you hurt me in this way

[jmrbug]

The video is short, straight to the point, very clear and easy to understand, AND homework was provided and examples were shown. Everything clicked with a single viewing of this video, great job and thank you!

[Z-Ren]

I am in a machine learning class and its not my strong suit, but this video explains everything 4x better than my professor! Nice job! +1 Sub

[eriol]

if only my teachers taught this concept in more practical manner, I wouldn't have been so confused. I remember learning this things during junior high school but never understood what's the purpose of learning this

[talkwitharindam]

Well explained keeping the simplicity ON.

[vandeljasonstrypper]

the first Indian youtuber I find it easy to understand

[gloriouswingsresearch]

can you explain how the formula is derived. That will make it more interesting

[bimanphil]

Nice examples are used, easy to understand

[raghavendraprabhu]

this one video was enough for me to subscribe your channel

[ashakalligotla]

Sir we need c and other programming language from you sir because ur the way of explanation is awesome...if u look into it it will be very helpful for us

[pseabrook]

Amazing video! Thanks for the clear explanations.

[anna-lenaarlt]

awesome video!! very clear explanations! :D

[robrobbins]

I've done the same simple linear regression in Excel, R Studio, Python, and C#. That really reinforces the material! But I think simple linear regression is really a common statistical method of analysis and therefore a fairly trivial example of machine learning. Still, it is the only method I have managed to understand so far!

[mickelodiansurname]

I had so much hoped that my exposure to math ended in 1992 after my finals, and I'd never see another formula that I actaully needed to use again. Yet, here I am in 2019 yet again sitting with a science calculator open on one screen, excel on another and listening to yet another asian guy twice as bright as I am.... Darn!

[excelscientist]

Brave, Great, no word to say -- One of the finest way to teach people, while i dont have any mathematical background

[mishaklovak]

Вот краткий обзор линейной регрессии:
- Линейная регрессия - это поиск наилучшей линейной зависимости, которая описывает некоторые данные, которые у вас есть.
- Важно отметить, что вы предполагаете, что между вашими зависимыми и независимыми переменными существует линейная связь
- Как только вы сделаете это предположение, вам необходимо выяснить конкретные линейные отношения
- Мы знаем, что общая форма линейного отношения выглядит так: Ax + By = C
- Мы хотим найти конкретную линейную связь, то есть конкретный набор A, B и C, такой, чтобы эта линейная связь лучше всего соответствовала нашим данным.

- Давайте подробно остановимся на том, что мы подразумеваем под «лучше всего соответствует нашим данным»
- Мы знаем, что, как только мы получим линейное отношение, это отношение позволяет нам предсказать нашу независимую переменную (y), учитывая нашу зависимую переменную (x)
- У нас есть некоторые выборочные данные (так называемые тестовые данные), где мы все знаем, ys для данного xs.
- Что если для каждого из наших образцов данных мы сравним известные y и y, которые мы получим, если вы используете наши конкретные линейные отношения?
- Итак, теперь наша цель стала: найти конкретные линейные отношения, которые приведут к тому, что ys будет максимально приближено к вашему фактическому ys в ваших выборочных данных.
- Если вы это сделали, то говорите, что нашли «наилучшую» линию подгонки.

- В приведенном выше примере мы рассматриваем ситуацию, когда у нас есть только одна независимая переменная, но у вас может быть много, и та же концепция будет по-прежнему применяться.
-Если у вас много независимых переменных, общая форма линейного отношения будет выглядеть следующим образом: Ax + By + Cz + ... = F, где A, B, C и F - параметры, вы хотите найти значения A, B, C и F, которые соответствуют вашим образцам данных лучше всего. Ничего не изменится, если вы добавите больше независимых переменных!

Главное, что нужно знать о линейной регрессии:
Вы предполагаете, что между вашими данными существует линейная связь, и затем вы находите конкретную линейную связь, которая наилучшим образом соответствует вашим данным.

Еще раз спасибо за еще одно очень веселое и информативное видео, мне это очень нравится!

[shubham]

is the equation for finding A and B same for any value taken in the data set or is it specific to this equation ?

[tacos]

thank you for using interesting examples like Pokemon vs urban density!

[arpitagec]

Great video! Where can I get the link of the linear regression implementation using python??
Please help