filmov
tv
how to find all of the primes

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
Where To Find All 5 Green Buttons in Blox Fruits | Green Button Locations
Find Score of an Array After Marking All Elements | 2 Approaches | Leetcode 2593 | codestorywithMIK
How to find all of your Gmail Accounts
HOW TO FIND ALL TOTEM LOCATIONS in FISCH! Roblox Fish
How to find All DEMIGUISE Moons to Upgrade Alohomora for level 2 and 3 Locks ► Hogwarts Legacy
UNLOCKING *NEW* SECRET ROBLOX FIND THE STICKMEN!? (ALL STICKMEN UNLOCKED!)
How to get ALL 200 MARKERS in FIND THE MARKERS || Roblox
How To Find All Of Your Gmail Accounts - find all of my Gmail accounts
You find all
How To Search and Find All Your Music Files in Windows 10
HOW TO FIND ALL 6 OF LANA’S ITEMS! QUEST 1 | #shorts #fyp #dti #dresstoimpress #roblox #trending
Fastest Method To find Earth Sprite in Fortnite - All Earth Sprite Locations
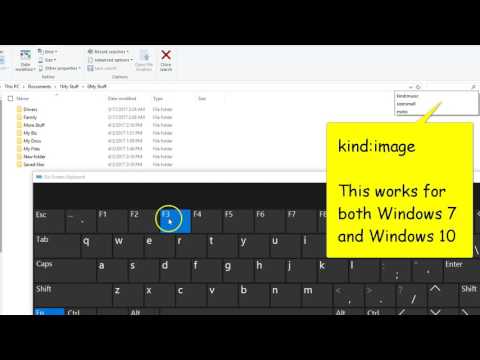
How To Search and Find All Your Pictures and images on Windows 10
How To FIND ALL 30 PRESENTS in Pet Sim 99 Christmas!
HOW TO FIND ALL NEW DOGS!
How to Find ALL of Your WHITETAIL DRINK ZONES (Detailed Zone Guide)!!! - Call of the Wild
FNAF: Security Breach - How To EASILY Find All Generators FAST In The Daycare
How to Search and Find All Your Videos, Movie and Video Files in Window 10
How To Find All Of The Hidden Statues.《In Bad Piggies》
CAN YOU FIND ALL?
We Find All 150 Markers!! Let's Play Find the Markers with Ryan & Mommy!!
HOW TO FIND ALL 96 STICKMEN in Find the Stickmen (96) | ROBLOX
HOW TO FIND ALL 81 FOODS in Secret Staycation | ROBLOX
How To Find ALL Insane, Extreme, Markerous Markers In Find The Markers! | Roblox Find The Markers
Комментарии
 0:00:45
0:00:45
 0:28:16
0:28:16
 0:01:45
0:01:45
 0:05:42
0:05:42
 0:15:55
0:15:55
 1:27:28
1:27:28
 1:12:16
1:12:16
 0:02:44
0:02:44
 0:00:08
0:00:08
 0:01:31
0:01:31
 0:00:59
0:00:59
 0:01:13
0:01:13
 0:01:56
0:01:56
 0:03:44
0:03:44
 0:04:18
0:04:18
 0:11:26
0:11:26
 0:02:29
0:02:29
 0:01:40
0:01:40
 0:06:38
0:06:38
 0:00:25
0:00:25
 0:07:45
0:07:45
 1:21:13
1:21:13
 0:59:36
0:59:36
 0:34:42
0:34:42