filmov
tv
Babylonian Method

Показать описание
More than 3000 years ago, the Babylonians invented a simple and incredibly accurate method for calculating square roots. This video explains how it works.
Babylonian Method
Babylonian Square Root
Calculating square roots easily IN 3 WAYS (BABYLONIAN and more)
EXPLAINED: Calculating square roots easily (BABYLONIAN and more)
Babylonian Algorithm and the Infinite Process
World's Fastest Square Root: Newton's Method
Fast, Accurate & simple method of Square root calculation | Babylonian Method
Computing Square Roots on Mechanical Calculator (Babylonian Method)
4000 Years Old Multiplication Trick
'Babylonian' method to convert denary to binary
Proof of Babylonian square root algorithm
BABYLONIAN SQUARE ROOT ALGORITHM Part 1
5.Babylonian numbers 1-9
The Babylonian Method for solving Quadratics (Works on ALL Quadratics)
++ Adventures - Babylonian method for square roots!
Babylonian Method of estimating square roots Math Algebra Jenn Burke
Solving Square Roots: Babylonian Method (Simplifying Math)
How to find square root of a number by using babylonian method?
Square Root Babylonian method
Babylonian Method to find square root of a number.
Programming - Ancient Babylonian Method to find Square Root of a Number Using Python
Babylonian Algorithm- Computing Square Root
Approximating Irrational Numbers Using the Babylonian Method
Finding the square root of a number using Babylonian method in JAVA
Комментарии
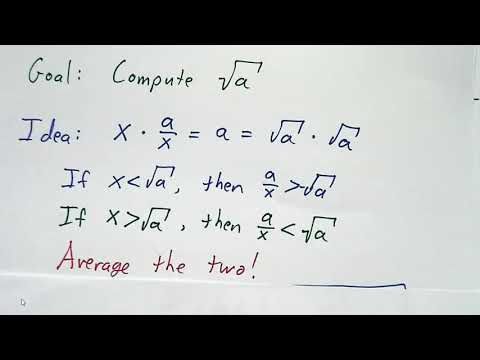 0:03:47
0:03:47
 0:09:35
0:09:35
 0:06:53
0:06:53
 0:09:29
0:09:29
 0:04:37
0:04:37
 0:02:18
0:02:18
 0:16:39
0:16:39
 0:06:25
0:06:25
 0:08:26
0:08:26
 0:04:08
0:04:08
 0:15:58
0:15:58
 0:28:02
0:28:02
 0:05:00
0:05:00
 0:11:04
0:11:04
 0:03:51
0:03:51
 0:10:42
0:10:42
 0:06:54
0:06:54
 0:01:49
0:01:49
 0:14:36
0:14:36
 0:15:46
0:15:46
 0:29:25
0:29:25
 0:06:09
0:06:09
 0:08:34
0:08:34
 0:04:11
0:04:11