filmov
tv
A Radical Equation | Integer Solutions

Показать описание
⭐ Join this channel to get access to perks:
#shorts #shortsvideo #shortsyoutube
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
#shorts #shortsvideo #shortsyoutube
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
A Radical Equation | Integer Solutions
Dividing a integer by a radical
Simplifying radicals multiplied by an integer
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
A Radical Equation #maths #exponential #education
A Radical Equation with a Radical Solution
How to Solve a Radical Equation (Involving a Quadratic Equation and Check)
Solving A Radical Equation in Three Ways
Алгебра №3 Часть №2: Алгебраические уравнения и неравенства...
Simplifying a Nice Radical Expression With Integers
How to Solve This Radical Equation with ease | You should Know the trick to solve
a radical equation #maths #solving
Find all positive integers x, y, satisfying a radical equation. Math Olympiad Challenge
Integer solutions to the Radical Equation √m + √n = √325 | Math Olympiad
Solve Radical (Square Root) Equations with Two Radicals
Equation Challenge: Solve a Radical Equation
A radical equation solved in three ways
Fractional Exponents
Find the sum of two positive integer variables that satisfy a radical equation.
Solving a Radical Equation
Learn how to simplify a radical
SOLVING RADICAL EQUATIONS #shorts #math #maths #mathematics
Solving Radical Equations & Identifying Extraneous Solutions
Simplify a radical expression with variables
Комментарии
 0:00:31
0:00:31
 0:02:16
0:02:16
 0:01:58
0:01:58
 0:03:11
0:03:11
 0:00:46
0:00:46
 0:05:09
0:05:09
 0:02:32
0:02:32
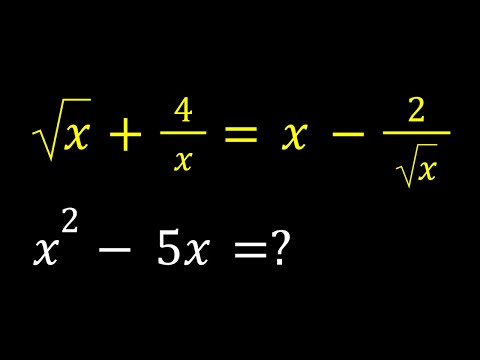 0:08:59
0:08:59
 2:11:40
2:11:40
 0:06:38
0:06:38
 0:05:15
0:05:15
 0:00:38
0:00:38
 0:07:46
0:07:46
 0:05:00
0:05:00
 0:09:31
0:09:31
 0:00:52
0:00:52
 0:09:55
0:09:55
 0:11:32
0:11:32
 0:10:40
0:10:40
 0:00:10
0:00:10
 0:04:09
0:04:09
 0:00:29
0:00:29
 0:05:45
0:05:45
 0:05:14
0:05:14