3.2 Smooth and Strongly Convex Functions

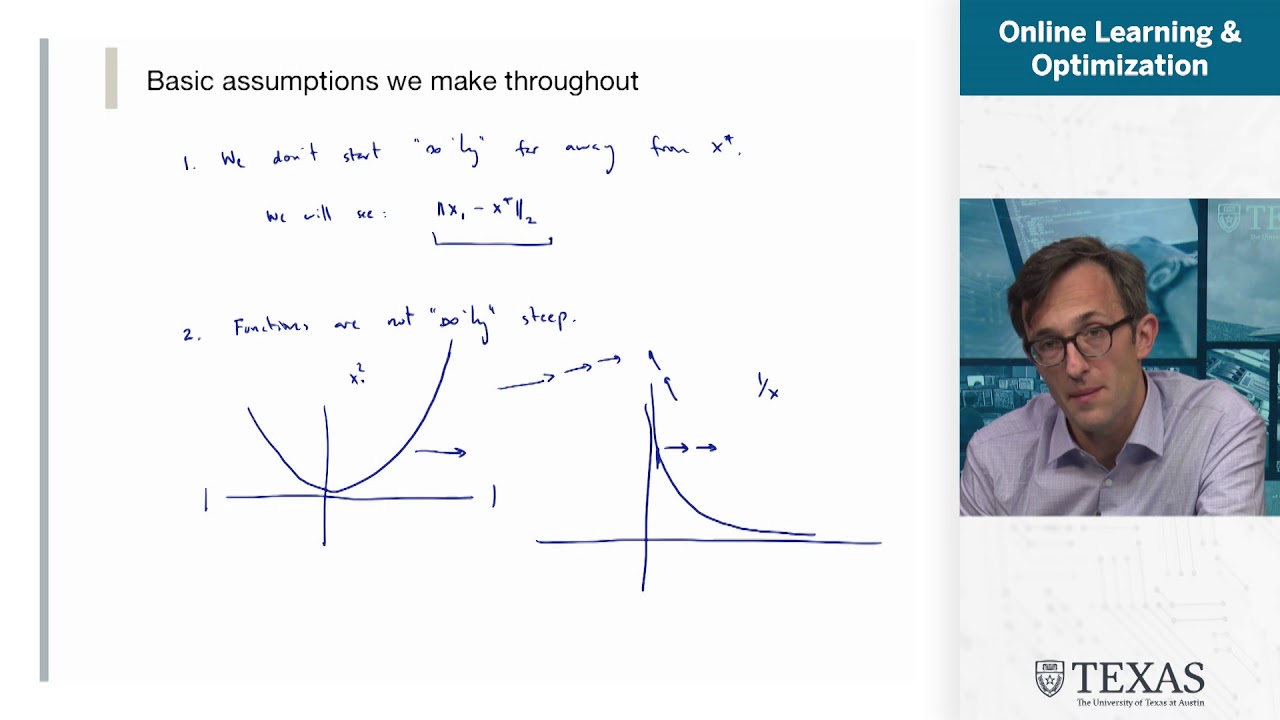
preview_player
Показать описание

  1. Constantine Caramanis
Рекомендации по теме
3.2 Smooth and 0:28:59

3.2 Smooth and Strongly Convex Functions

[W2-2] strongly convex 0:10:52

[W2-2] strongly convex function and smooth convex function

3.3 Properties of 0:32:22

3.3 Properties of Smooth and Strongly Convex Functions

[W2-5] convergence rate 0:13:07

[W2-5] convergence rate of strongly convex and smooth functions

Gradient Descent: Smooth 0:11:52

Gradient Descent: Smooth Strongly Convex Functions

Strictly convex functions, 0:05:05

Strictly convex functions, unique global minimum, optimization algorithms, stochastic gradient desc

[W2-6] Q&A Gradient 0:05:53

[W2-6] Q&A Gradient norm and strongly convex

Part 5 strong 0:12:19

Part 5 strong convexity

Stochastic Approximation of 0:09:00

Stochastic Approximation of Smooth and Strongly Convex Functions

Preliminaries: Strong Convexity 0:20:28

Preliminaries: Strong Convexity

Convex Optimization Full 1:14:09

Convex Optimization Full Summary

【Lecture】L3 Convergence rate 1:53:06

【Lecture】L3 Convergence rate and strongly convex functions

Jean-Francois Aujol - 1:00:35

Jean-Francois Aujol - FISTA is a geometrically optimized algorithm for strongly convex functions

ECO760A : Mathematical 0:18:39

ECO760A : Mathematical Analysis for Economics : Lecture 14a : Strong Convexity

Restricted Strong Convexity 0:27:57

Restricted Strong Convexity Implies Weak Submodularity, Alex Dimakis

Part 4: beta 0:14:58

Part 4: beta smooth functions

Optimization in Machine 2:54:50

Optimization in Machine Learning: Lecture 2 (Convex Functions Cont, Analysis of Gradient Descent)

1.1 Introduction to 0:08:45

1.1 Introduction to Optimization and to Me

unexpected neet result 0:00:14

unexpected neet result #physicswallah #yakeen2.0 #competitionwallah

Week 2: Lecture 0:43:54

Week 2: Lecture 7: Implications of strong convexity

LM1.2 - Concavity/Convexity 0:09:20

LM1.2 - Concavity/Convexity of multi-variable functions

VA & OPT: 1:05:43

VA & OPT: The Boosted Difference of Convex Functions Algorithm

Xuyang Wu - 0:29:29

Xuyang Wu - Distributed Approximate Methods of Multipliers for Convex Composite Optimization

Strictly convex normed 0:18:32

Strictly convex normed space definition and examples,

Комментарии
Автор

For anyone interested in understanding smooth/strong convexity conceptually:
A function is smoothly convex if at any point you can fit a quadratic on it
A function is strongly convex if at any point you can fit a quadratic underneath it

gt_money
Автор

Thank you for sharing such a good video!

andrewmeowmeow
Автор

thank you so much this is really useful thanks for saving my finals and everything

lindseyfeng
Автор

Assumptions: 5:30
Beta-Smooth(Lipschitz continuous): 8:00
Beta-smooth -> monotone -> convex: 10:31
Beta-smooth -> quadratic upper bound 15:48
Alpha-Strong convexity -> quadratic lower bound: 22:43

xinlunzhao
Автор

Thanks so much for these detailed explanations. It really helps.

salwamostafa
Автор

Does the definition of the quadratic upper bound assume that f is convex? from what I understand that f is not required to be convex just smooth, but to derive the quadratic upper bound we define the function g and proved that g is convex.

Another question, why did we define function g in that exact shape?

eyadshami