filmov
tv
Квантовые вычисления #6 - Запутанные состояния

Показать описание
Поддержите канал:
Квантовые вычисления #6 - Запутанные состояния
Что такое квантовые вычисления? Душкин объяснит
Вычисления на квантовых компьютерах
Что такое КВАНТОВЫЙ компьютер? | РАЗБОР
Квантовый мир.
КВАНТОВЫЕ ВЫЧИСЛЕНИЯ. Кубиты, суперпозиция, запутанность, квантовые вентили и алгоритм Гровера....
Леонид Прядко: Введение в теорию квантовых кодов, квантовые цепи и протоколы квантовой телепортации...
Квантовые вычисления #5 - Многокубитные гейты
А.А. Тропов. Однофотонные источники для квантовой информатики...
Моисеев С.А. Квантовая память для квантовых вычислений и коммуникаций...
Александр Березутский: Введение в тензорные сети для квантовых вычислений...
Квантовые вычисления
Квантовая теория доказывает, что вы никогда не умираете!...
БЕЗ ЭТОГО НЕ СДАТЬ ЕГЭ по Химии — Электронная конфигурация атома...
Станислав Страупе | Будущее квантовых вычислений
Квантовые вычисления, связь, измерения. Состояние дел
Электронные конфигурации атомов. Химия – просто
Станислав Страупе 'Линейно-оптические системы квантовых вычислений'...
Что может взломать квантовый компьютер?
Алексей Федоров: Квантовые вычисления: новые рубежи в науке и цифровых технологиях...
Квантовые числа. Принцип Паули, правило Гунда (Хунда) и правило Клечковского. 2 часть. 10 класс....
Миф о Квантовом компьютере. Провал о котором молчат все...
Что не так с квантовой запутанностью? Квантовые эффекты простым языком!...
Самые ХАРДКОРНЫЕ ПАРАДОКСЫ квантовой физики!
Комментарии
 0:09:45
0:09:45
 0:16:00
0:16:00
 1:18:27
1:18:27
 0:11:10
0:11:10
 2:35:28
2:35:28
 0:08:32
0:08:32
 2:07:13
2:07:13
 0:12:46
0:12:46
 1:27:31
1:27:31
 1:08:36
1:08:36
 0:11:11
0:11:11
 0:36:35
0:36:35
 0:11:15
0:11:15
 0:17:19
0:17:19
 0:18:36
0:18:36
 0:23:30
0:23:30
 0:05:16
0:05:16
 0:41:14
0:41:14
 0:53:30
0:53:30
 0:56:33
0:56:33
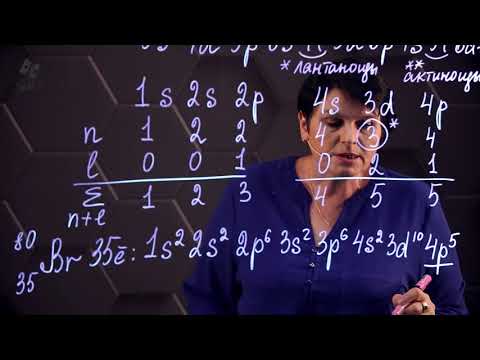 0:18:08
0:18:08
 0:27:09
0:27:09
 0:21:36
0:21:36
 0:26:02
0:26:02