filmov
tv
Relativity 109b: Gravitational Waves - Linearized Gravity / Weak Gravity

Показать описание
Other Sources:
0:00 Introduction to Linearized Gravity
2:26 Inverse Metric
5:03 Connection Coefficients
6:15 Riemann Tensor
7:39 Ricci Tensor
8:53 Ricci Scalar
9:58 Einstein Tensor
13:02 Summary
Relativity 109b: Gravitational Waves - Linearized Gravity / Weak Gravity
Relativity 109d: Gravitational Waves - Transverse-Traceless Gauge (Plus and Cross Polarizations)
Relativity 109c: Gravitational Waves - Wave Derivation (The Lorenz Gauge)
Relativity 109e: Gravitational Waves - How Gravitational Wave Affect Free Particles
Relativity 109a - Gravitational Waves: Introduction (LIGO, Wave Equation)
Gravitational wave (Einstein linearization theory)
General Relativity, Lecture 15: gravitational waves and cosmology
General Relativity, Lecture 24: Gravity Waves. Linearized General Relativity.
Generation of Gravitational Waves from an Axisymmetric Oscillating Quadrupole Moment
Gravitational Waves with Professor Bernard Schutz
Colloquium: Zvi Bern: From Quantum Scattering Amplitudes to Gravitational Waves
Generation of Gravitational Waves by a Rotating Quadrupole Source
Making (gravitational) waves
6.1 Solving the Einstein equations for gravitational waves
GR lecture 44 -- Gravitational Waves I
Gravitational waves
16. Gravitational radiation I
First Observation Of Gravitational Waves #spacescience #gravitationalwaves #astrophysics
Visualizations of Gravitational Waves' transverse Polarizations: Plus, Cross, Circular
Karl Schwarzchild : The man who predicted black hole by Einstein's equations...
109| Orbital Precession of the S2 Star Around the Galactic Center (Non-Relativistic Explanation)
The Mathematics of Gravitational Radiation part1
Angelo Ricciardone: 'Stochastic Gravitational Wave Background' - Lecture I
6 4 1 Propagation Of Gravitational Waves
Комментарии
 0:13:51
0:13:51
 0:21:05
0:21:05
 0:23:55
0:23:55
 0:18:30
0:18:30
 0:15:47
0:15:47
 0:00:16
0:00:16
 0:43:33
0:43:33
 1:18:54
1:18:54
 0:00:07
0:00:07
 0:12:39
0:12:39
 1:21:17
1:21:17
 0:00:06
0:00:06
 1:02:50
1:02:50
 0:15:21
0:15:21
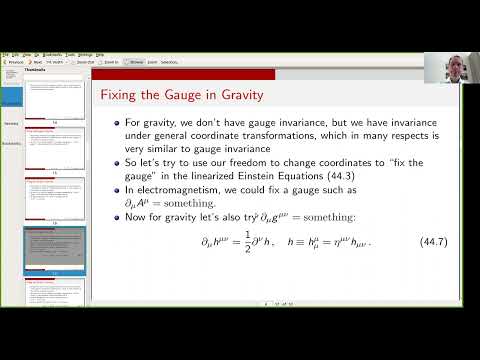 0:22:23
0:22:23
 1:06:40
1:06:40
 1:25:12
1:25:12
 0:00:06
0:00:06
 0:01:01
0:01:01
 0:00:20
0:00:20
 0:00:07
0:00:07
 1:19:38
1:19:38
 2:01:02
2:01:02
 0:41:02
0:41:02