filmov
tv
Produit vectoriel

Показать описание
Produit vectoriel
produit vectoriel : règle de la main droite
Comment calculer le produit vectoriel de deux vecteurs
Le produit vectoriel en Sciences de l'Ingénieur (PCSI/PTSI/MPSI)
Comment calculer le produit vectoriel de deux vecteurs - exercice corrigé
Tuto physique : produits scalaire et vectoriel
Le produit vectoriel, introduction
Comment calculer le produit vectoriel de deux vecteurs
'Coplanar Vectors in Physics & Math: Key Concepts & Examples with Experiment'
Le produit vectoriel, interprétation géométrique et produit mixte
Produit vectoriel : Partie I
Introduction au produit vectoriel
Le produit vectoriel, règle de calcul
Le produit vectoriel de deux vecteurs || expression analytique #terminale Spé
Différences entre le produit scalaire et le produit vectoriel
LE COURS : Produit scalaire - Première
3.07 Calculs métriques et angulaires - Produit vectoriel de deux vecteurs de l'espace
Pourquoi le produit vectoriel en mécanique?
Méthodologie - Produit vectoriel à l'aide d'une figure de calcul
Produit vectoriel
Savoir-faire: produit vectoriel de deux vecteurs du plan
Produit vectoriel - La géométrie dans l'espace
Le produit vectoriel, propriétés
Méthodes de calcul des produits vectoriels
Комментарии
 0:06:15
0:06:15
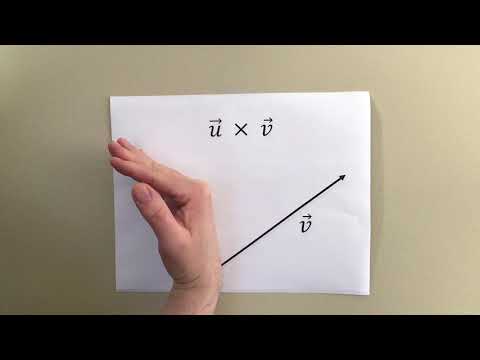 0:01:44
0:01:44
 0:04:37
0:04:37
 0:09:47
0:09:47
 0:12:47
0:12:47
 0:14:18
0:14:18
 0:37:05
0:37:05
 0:10:01
0:10:01
 0:08:09
0:08:09
 0:17:38
0:17:38
 0:10:05
0:10:05
 0:18:13
0:18:13
 0:23:12
0:23:12
 0:16:05
0:16:05
 0:10:38
0:10:38
 0:18:42
0:18:42
 0:02:52
0:02:52
 0:17:43
0:17:43
 0:06:51
0:06:51
 0:09:21
0:09:21
 0:01:58
0:01:58
 0:31:48
0:31:48
 0:28:46
0:28:46
 0:22:53
0:22:53