filmov
tv
Solving Absolute Value Equations Containing TWO Absolute Value Expressions - Example 1
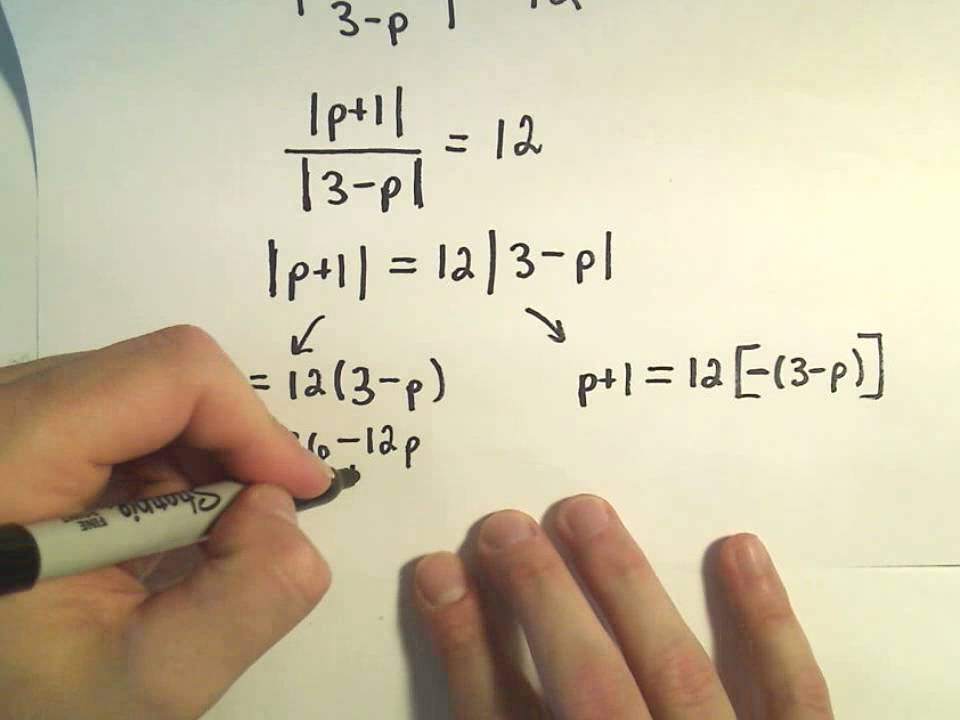
Показать описание
How To Solve Absolute Value Equations, Basic Introduction, Algebra
Solving an Absolute Value Equation
How To Solve Absolute Value Equations
Solving an Absolute Value Equation
Absolute Value Equations | An Introduction | Math with Mr. J
Solving Absolute value equations with a variable on both sides
Absolute Value Equations with No Solutions
Solving Equations w/ Absolute Values Algebraically ('By Cases')
Solve an Absolute Value Equation
Solving an Absolute Value Equation with no Solution - Free Math Videos
Extraneous Solutions of Absolute Value Equations
Absolute value equations | Linear equations | Algebra I | Khan Academy
Solving Absolute Value Equations Containing TWO Absolute Value Expressions - Example 3
How to Solve an Absolute Value Equation with Absolute Values on Both Sides
Solving Advanced Absolute Value Equations
Solving Absolute Value Equations with Ease
How to Solve Absolute Value Equations | Math with Mr. J
Example: Solving an Equation Involving Absolute Value
Solving an Absolute Value Equation with Two Absolute Value Expressions (Example)
Solving an Absolute Value Equation with Two Solutions
Absolute Value Inequalities - How To Solve It
Easily Solve an Absolute Value Equation With a Fraction
Equation with Two Absolute Values
Solving Absolute Value Equations #mathteachergon #algebra #solvingequations #AkosiTeacherGon
Комментарии
 0:04:21
0:04:21
 0:05:00
0:05:00
 0:20:53
0:20:53
 0:02:40
0:02:40
 0:10:54
0:10:54
 0:03:40
0:03:40
 0:03:17
0:03:17
 0:09:42
0:09:42
 0:02:39
0:02:39
 0:02:13
0:02:13
 0:11:24
0:11:24
 0:10:41
0:10:41
 0:03:53
0:03:53
 0:03:09
0:03:09
 0:40:33
0:40:33
 0:07:17
0:07:17
 0:05:21
0:05:21
 0:02:03
0:02:03
 0:06:50
0:06:50
 0:01:12
0:01:12
 0:12:40
0:12:40
 0:02:54
0:02:54
 0:01:47
0:01:47
 0:01:00
0:01:00