filmov
tv
Corollaries of Lagrange's Theorem in Group Theory
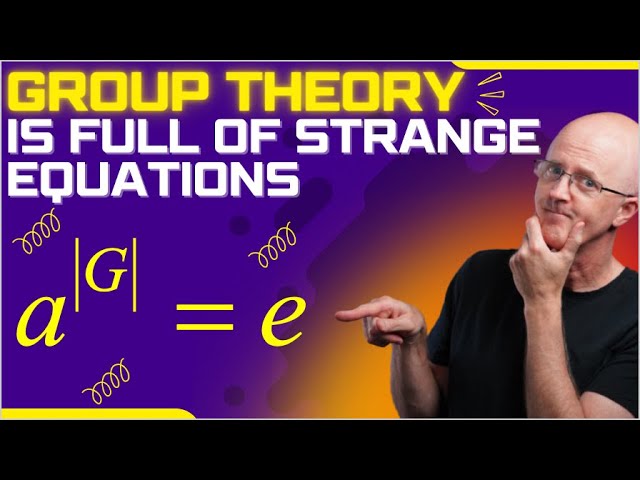
Показать описание
Lagrange's Theorem is so important in Group Theory from Abstract Algebra! Some important corollaries of Lagrange's Theorem include: 1) The index of a subgroup H in a finite group G is |G|/|H|. 2) If G is a finite group, the order of each element in G divides the order of G. 3) Every group of prime order p is isomorphic to ℤp (the group of integers under addition modulo p). 4) If G is a finite group and "a" is an element of G, then a^|G|=e (raising any group element to the power of the order of the group gives the identity element). 5) Fermat's Little Theorem: for every integer "a" and every prime p, a^p mod p equals a mod p.
Links and resources
===============================
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Links and resources
===============================
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Corollaries of Lagrange's Theorem I - Chapter 5 - Lecture 6
Corollaries of Lagrange's Theorem in Group Theory
Corollaries of Lagrange's Theorem II - Chapter 5 - Lecture 7
Group Theory: Corollaries of Lagrange’s Theorem . lect. 7
Abstract Algebra. Corollaries of Lagrange's Theorem
Corollaries of Lagrange's theorem III - Chapter 5 - Lecture 8
52 A Corollary of Lagrange's Theorem
Properties of Cosets in Group Theory | Lagrange's Theorem and Corollaries
MATH 430 — 14: Corollaries to Lagrange’s Theorem
Index of a Subgroup Corollary of Lagrange 's Theorem
An Important Corollary on Lagrange's Theorem about Primitive Roots of Primes
Mo.S.K. | Lagrange's Theorem and Corollary of Orders :o | RGT 5 Part 2
corollaries about lagrange theorem
Corollary of Lagrange's Theorem|| GROUP THEORY #41||
COROLLARY OF LAGRANGES THEOREM
AJP501LECTURE9(Lagrange theorem and it's corollaries)
GT3. Cosets and Lagrange's Theorem
Lagrange's Theorem - Chapter 5 - Lecture 5
Cosets and Lagrange’s Theorem - The Size of Subgroups (Abstract Algebra)
3.2 Lagrange's Theorem
Prove Lagrange’s Corollary. The order of a finite group is divisible by the order of any element
138 - Lagrange's Theorem and Corollaries
Lagrange's Theorem (Number of Solutions of a Polynomial Congruence)
Lagrange's Theorem
Комментарии
 0:10:29
0:10:29
 0:09:41
0:09:41
 0:14:08
0:14:08
 0:23:25
0:23:25
 0:20:15
0:20:15
 0:11:31
0:11:31
 0:06:29
0:06:29
 0:44:19
0:44:19
 0:17:06
0:17:06
 0:02:13
0:02:13
 0:25:35
0:25:35
 0:07:09
0:07:09
 0:21:17
0:21:17
 0:08:24
0:08:24
 0:09:15
0:09:15
 0:52:49
0:52:49
 0:16:34
0:16:34
 0:13:14
0:13:14
 0:09:19
0:09:19
 0:13:39
0:13:39
 0:04:03
0:04:03
 0:12:18
0:12:18
 0:23:48
0:23:48
 0:16:04
0:16:04