filmov
tv
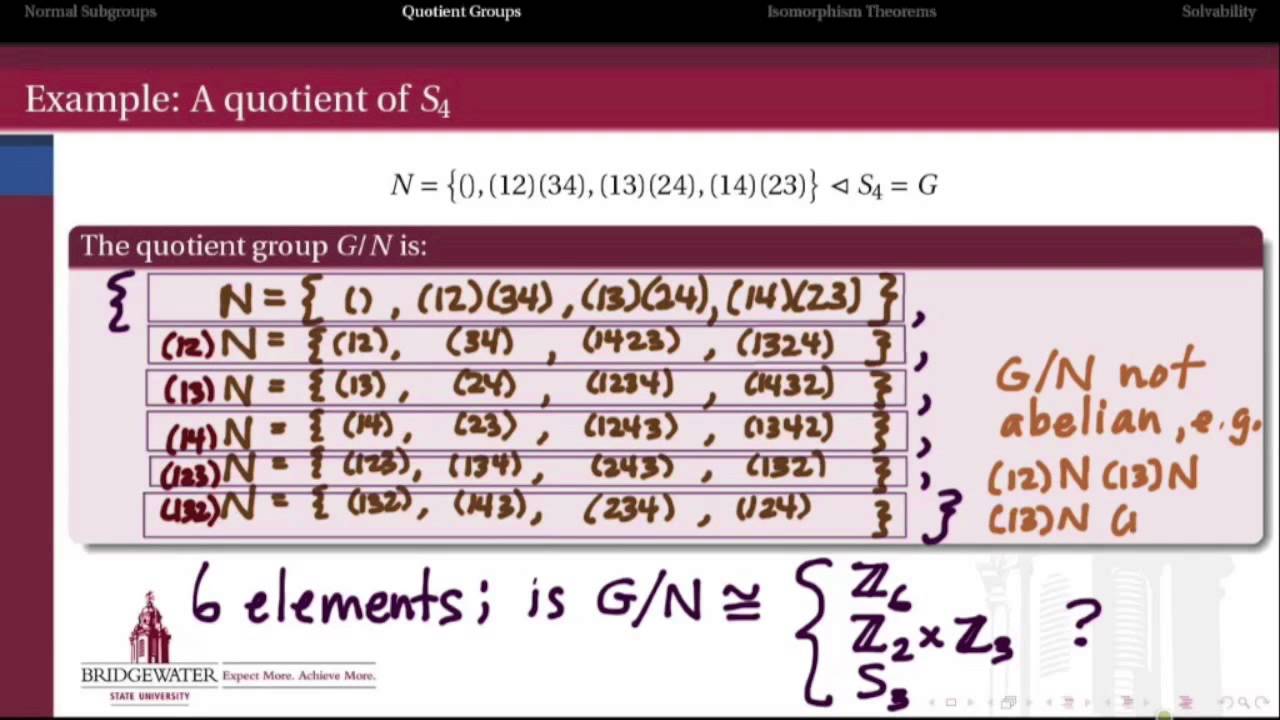
302.4A: Quotient Groups
Показать описание
Reviewing the quotient of a group by a normal subgroup. The First and Fourth Isomorphism Theorems.
302.I.4b: Discriminants - What Can They Tell Us?
302.5B: The Alternating Group
302.7D: What is a Galois Group?
302.6A: Conjugacy Motivation
Gaussian Integers with Norm 1 are Units
302.S4: Normal Extensions
302.7C: La Ideé du Galois
4th-Grade Math - 4A - Ch. 6 D - Multiply a Fraction and a Whole Number - pgs. 297-302
#Edu501#CS302#PHy302#Psy402#psy504#Bio504#Edu406 #All #Final term papers#Top #channel
Lecture 12. Galois Group of a Polynomial
302.S3b: Finding Minimal Polynomials
Ek jhatke mein ho jayega The End 💔
AUD: Corporate Governance and Financial Risk Management: McDonald's SOX reporting
L 28 Example of Factor Ring | Quotient Ring | Ring theory and Linear Algebra 1 | B Sc Hons Maths DU
302.7A: Polynomials & their Roots
Stanley Xiao - Some curious facts about binary quartic forms with small Galois group
Lecture 11, Part 2
Modular Category O and Parity Sheaves on Flag Varieties Pt. 1
Field Extensions and Roots of Polynomials (Algebra 3: Lecture 8 Video 2)
Simple Extensions (Algebra 3: Lecture 8 Video 3)
Prof. Andy Schultz - Galois embedding problems, part 1
Algebra of Matrices || Inverse of a Matrix || By Elementary Transformation || Gauss-Jordan Method
24 Index of H in G
Integers in Quadratic Fields
Комментарии
 0:05:12
0:05:12
 0:14:31
0:14:31
 0:14:51
0:14:51
 0:08:00
0:08:00
 0:05:07
0:05:07
 0:09:25
0:09:25
 0:12:07
0:12:07
 0:16:01
0:16:01
 0:01:12
0:01:12
 0:49:51
0:49:51
 0:09:24
0:09:24
 0:00:21
0:00:21
 0:11:14
0:11:14
 0:15:17
0:15:17
 0:10:45
0:10:45
 0:44:25
0:44:25
 0:30:20
0:30:20
 0:38:49
0:38:49
 0:26:20
0:26:20
 0:21:48
0:21:48
 0:25:14
0:25:14
 0:20:39
0:20:39
 0:36:31
0:36:31
 0:19:24
0:19:24