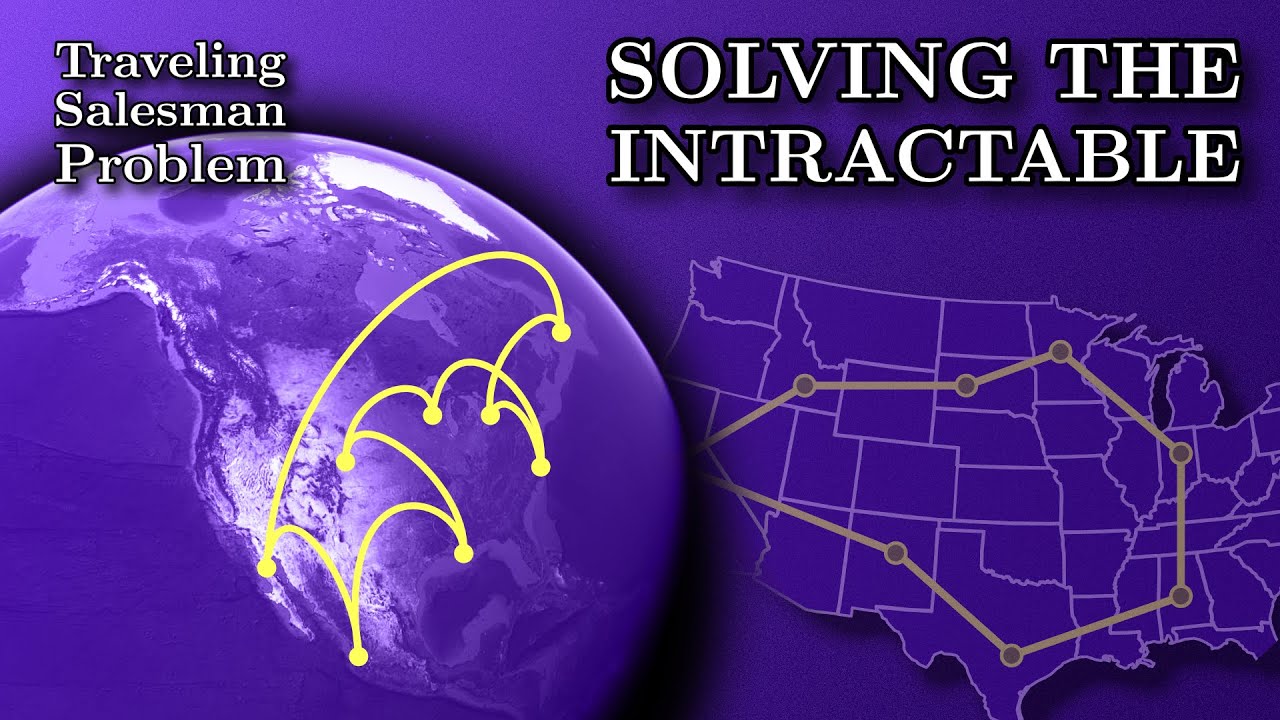
The Traveling Salesman Problem: When Good Enough Beats Perfect

The Traveling Salesman Problem (TSP) is one of the most notorious problems in all of computer science. In this video, we dive into why the problem presents such a challenge for computer scientists and some of the clever methods used to solve the problem.

We start with showing why all brute force solutions and even optimizations to get exact solutions can't reliably be used for large instances of the problem. We then proceed to discuss some heuristic based approaches such as nearest neighbors, greedy, and Christofides to get solutions that are reasonably close to the optimal solution.

But after finding a candidate solution, we also show how one might improve this solution via local search. We discuss some interesting algorithms for tour improvements including 2-opt, random swapping, and 3-opt improvements. Finally, we show some clever ways to analyze the search space, including simulated annealing and ant colony optimization.

Chapters:
0:00 Intro
1:27 Problem Definition
2:27 Why Finding Optimal Solution Is Practically Impossible
5:35 Nearest Neighbor Heuristic
6:59 Lower Bounding TSP
11:03 Greedy Heuristic
12:06 Christofides Algorithm
16:11 Sponsor (CuriosityStream)
17:15 Tour Improvements
21:13 Simulated Annealing
24:14 Ant Colony Optimization
28:25 Conclusion

Animations created jointly by Nipun Ramakrishnan and Jesús Rascón.

References:

This video wouldn't be possible without the open source library manim created by 3blue1brown and maintained by Manim Community.

Music in this video comes from Jesús Rascón and Aaskash Gandhi

Socials:

Big thanks to the community of Patreons that support this channel. Special thanks to the following Patreons:
Andjela Arsic
Andreas
Adam Dřínek
Burt Humburg
Brian Cloutier
Eugene Tulushev
kerrytazi
Matt Q
Mutual Information
Ram K
Richard Wells
Sebastian Gamboa
Winston Durand
Zac Landis

[austinbutts]

"Sometimes things have to get worse before they get better."

I didn't expect life wisdom to come from a video on heuristic optimization algorithms. A surprise to be sure, but a welcome one.

[KazeSenshi]

I know the optimal algorithm for a graph with two nodes.

[Nononoya]

TSP is a NP hard problem but so is making this video. Every seconds of the video I see an exponential effort invested. Thank you so much!

[wafikiri_]

In the '80's, I used a different strategy to solve this problem, just for my satisfaction. I based my solution on the way Nature would create an inner expanding bubble until touching all the nodes with minimal tensional energy. I used Basic in an 80286 PC, with about 100 random nodes. A short program with less than 100 lines of code was enough to get satisfactory results.
Edit: minor grammatical correction (English is not my first language, sorry for that).

[breckandolley]

I'm quite impressed that you managed to avoid mentioning entropy while discussing the annealing approach and the pheromone approach. I once tried to explain pheromone optimization to a friend of mine who wasn't familiar with using entropy to backtrack a search, and I simply wasn't able to explain the process. Well done!

[Mutual_Information]

Been excited for this video for awhile. I’ve heard of TSP superficially many times.. but never got a deep dive like this before. Very motivated, exceptionally beautiful and naturally narrated. Content like this is the gem of YouTube.

Just to add: As impossible as this problem is.. it’s wild to know we have a record solution with a tour length of 7.5+ billion.

[brain]

So I had this job at a water-selling firm (pumping artesian water source and distributing it either in bottles or through dispensing machines). I took care of machine maintenance and also the logistics of refilling the machines with water. Basically making routes for the drivers that did it. Then some time later got into coding trying to change my career, and in search of ideas to build a portfolio, had this "brilliant" idea of making a routing algorithm. "Should be easy, I can do the routes with my eyes closed by now, just need to put the logic in my brain into code". Or so I thought. After some research, you guessed it, it turned out that I was trying to tackle the TSP. After lots of hours trying to get it to output routes that actually make sense scaled it down to a small web-app that just sorted stuff by priorities, while still doing routing myself, still saved some time and made a nice entry into the portfolio.

[EricKolotyluk]

I have an MSc in Computing Science, but I have never seen a treatment of TSP and friends as beautiful as this. Thank you.

[tenet-rotas]

Never would I have thought that there is a connection between crystallurgy and the travelling salesman problem. What a beautiful video. Thank you for making this accessible for everyone! <3

[rubensleite]

I will definitely apply this to my thesis problem: Point cloud registration and 3D reconstruction. Thank you very much.

[CursedByManga]

Never knew there were so many similarities between solving TSPs and reinforcement learning!
Simulated annealing is so similar to the explore-exploit and the ant colony optimization also reminds me so much of genetic algorithms and reinforcement learning😻


Cool video!!

[tkzubaran]

PSPACE problems, common in planning, are arguably "harder", as TSP is "only" NP-hard.

[Arthurt]

It's interesting to see how a "simplifyed" (two way edges, linear paths) can become arbitrarily hard to solve. Imagine bringing this problem to a urban scenario, where edges are streets that are not necessarily 2 way and are non linear and trafic is involved.

[jimboli]

In love with the new intro. Amazing content as always! Doing computer science proud!

[ThePlayfulJoker]

Wow, that's a lot better than the 10 slides I got in university for this problem. Even took me less time to go through your video because it made so much more sense. Online universities with teachers like you would be so much better for everyone involved. Mad respect for you to make videos at this level of quality!

[rohitd]

Great insight on TSP. The research is vast and the information is often overwhelming.. but the way everything seems connected at the end is just amazing. Great intuitive ways to solve the TSP, would love to see more content on NP hard and NP complete problems. I started watching your content almost 2 years back when I first saw your ‘Towers of Hanoi’ video. Informative and concise.. love the animations <3

[thomascoolidge]

I did a report in Linear Algebra discussing using Adjacency Matrices to find paths from any point to any other point by raising matrices to their power step by step. I managed to make it work for minimum hop count and shortest path between two points. Unfortunately it doesnt solve the TSP because it does not go back to it starting point.. only that it can hit every point. We had another idea of using something similar to what we called gravitic weighting to image creating the shortest path by picking any point and then "lifting it" and seeing the other points fall based upon distance.. we ran into problems with pruning of ineffecient routes.. if we could identify routes that were not going to be used we think it would have worked.. unfortunately our advisor didnt seem to care to help us at all... to him TSP was just an impossible problem and we were waisting our time.

[kaishang]

your videos are always a treat and often expose me to more knowledge that I didn't know exists before. thank you.

[ricardocardoso]

This video was very well done! I come from a data science background, and so I was more familiar with the traveling salesman problem in the context of evolucionary optimization and multi objective optimization. The heuristic aproaches presented in this video are super interesting, and the presentation is amazing, it was really easy to understand.

[tellurian]

One of my favorite approximations is using a blob-like shape that stretches itself to just barely touch all the nodes while taking up as little space as possible, and then going around the edges of the blob.