filmov
tv
Chain Rule Surprise
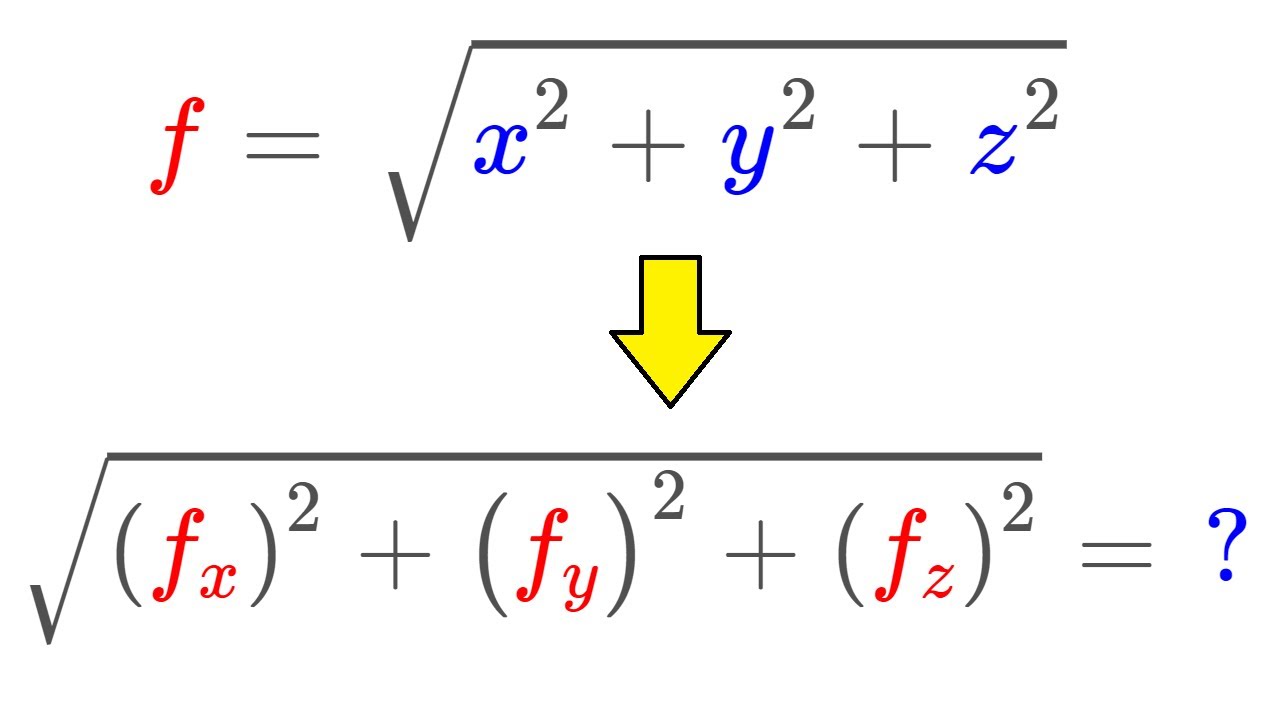
Показать описание
In this video, I present a neat result I have noticed when calculating some partial derivatives! Is it a coincidence? I'm not sure! Enjoy!
Chain Rule Surprise
Chain rule
A Proof of the Chain Rule
How to use the Chain Rule - Calculus: Differentiating
The Chain Rule for Differentiation Examples
14.5: The Chain Rule
DIfferentiation: Example of Chain rule
Differentiation 1.4 Chain rule
SURPRISE STORM INCOMING!
She Gets A SURPRISE! 😱
Multivariable Calculus 7 | Chain, Sum and Factor rule
Differentiating Log Functions w/ Chain Rule
31 Chain Rule for Derivatives
8a. Problems. Chain Rule
Calculus - Chain Rule - Hard Problem 6
Implicit differentiation example question
Mastering the Chain Rule Forming Expressions for z(x(t), y(t)) and z(x(s,t), y(s,t))
Calculus I: Chain Rule Examples
Calculus 30 2.6 Chain Rule
Chain rule and polar coordinates, order I
BFF Gifts. Undying Friendship #bff #gift #surprise
Examples: The Chain Rule
Business Calculus - The Chain Rule
Tack’s surprise for Poom 🌹❤️ The baby couple 🥹 #thesignseries #tackpoom
Комментарии
 0:07:02
0:07:02
 0:15:40
0:15:40
 0:08:33
0:08:33
 0:05:53
0:05:53
 0:16:31
0:16:31
 0:31:48
0:31:48
 0:30:54
0:30:54
 0:05:50
0:05:50
 0:05:43
0:05:43
 0:00:23
0:00:23
 0:12:22
0:12:22
 0:13:33
0:13:33
 0:08:22
0:08:22
 0:39:35
0:39:35
 0:03:49
0:03:49
 0:00:34
0:00:34
 0:07:14
0:07:14
 0:21:23
0:21:23
 0:23:39
0:23:39
 0:10:07
0:10:07
 0:00:16
0:00:16
 0:25:16
0:25:16
 0:14:37
0:14:37
 0:01:00
0:01:00