filmov
tv
Magic Square Construction Algorithm N × N

Показать описание
Magic square Construction 3×3. It is a matrix in which addition of every row , every column and both diagonals is same.
Magic Square Construction Algorithm N × N
The MAGIC Square Problem (Coding Interview Question)
Quick Vedic Magic Square Construction Algorithm for Any N×N 8X8 12X12 | Easy Math Trick'
Magic Square Party Trick - Numberphile
3 by 3 Magic Squad | 3x3 Magic Square | Two Easy methods on 3x3 Magic Square | Magic Square 3*3
Unlocking the secrets of Magic Square puzzles
Magic Squares In Grid - Leetcode 840 - Python
Quick Java Magic Matrix HackerRank Solution
Program To Generate Magic Square Matrix For Any Value Of N
MAGIC SQUARE Code Algorithm Explaination
5 By 5 Magic Square | 5x5 magic Square | magic square 5x5 | magic square
Introduction to the Proof of Siamese Magic square construction #SiameseMethodProof #magicsquares
Program Demonstrating Magic Squares
Construction of odd-magic-squares | De la Loubère Method
Scratch Challenge: Magic Squares
The Korean king's magic square: a brilliant algorithm in a k-drama (plus geomagic squares)
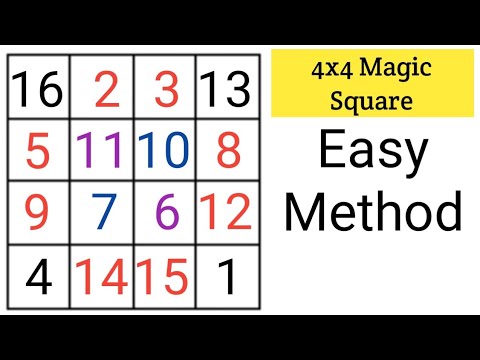
4x4 magic square | 4 by 4 magic Square | magic square | magic square 4x4 | Maths magic tricks
How to Construct Odd Order Magic Squares
Magic Squares of Squares (are PROBABLY impossible) - Numberphile
Java Competitive Coding 02: HackerRank Magic Squares Challenge
Magic Squares - Constructing 'Odd order' ones
Magic Square Hit and Trial 04
HackerRank | Problem Solving | Forming a magic square
Java Tutorial: How to Generate a Magic Square of Odd Dimensions
Комментарии
 0:21:01
0:21:01
 0:07:24
0:07:24
 0:13:04
0:13:04
 0:03:58
0:03:58
 0:02:05
0:02:05
 0:11:21
0:11:21
 0:21:12
0:21:12
 0:10:53
0:10:53
 0:11:48
0:11:48
 0:06:38
0:06:38
 0:03:00
0:03:00
 0:09:19
0:09:19
 0:05:27
0:05:27
 0:10:39
0:10:39
 0:19:59
0:19:59
 0:33:25
0:33:25
 0:01:59
0:01:59
 0:01:00
0:01:00
 0:33:39
0:33:39
 0:07:36
0:07:36
 0:04:49
0:04:49
 0:12:20
0:12:20
 0:09:32
0:09:32
 0:12:54
0:12:54