filmov
tv
Inner Product Spaces - 1

Показать описание
We wish to find an additional structure on a real vector space in which we can talk of the length of a vector and the angle between (non-zero) vectors. We look at R2 and R3 for inspiration. Along with the law of cosines in the trigonometry of triangle, we arrive at the notion of the dot product on R2. We look at it generalization to Rn.
Timestamp provided by Ishwarya.
00:00 Introduction
0:50 Aim of this lecture series
6:32 Discussion about the Metric Structure on a Vector space V
8:24 Length of a vector
12:07 Angle between two vectors (complex version)
23:14 Motivation for dot product
27:27 Dot product
28:37 Cauchy Schwarz Inequality
30:48 Angle between two vectors using law of cosines
36:33 End note
Timestamp provided by Ishwarya.
00:00 Introduction
0:50 Aim of this lecture series
6:32 Discussion about the Metric Structure on a Vector space V
8:24 Length of a vector
12:07 Angle between two vectors (complex version)
23:14 Motivation for dot product
27:27 Dot product
28:37 Cauchy Schwarz Inequality
30:48 Angle between two vectors using law of cosines
36:33 End note
Linear Algebra: Inner Product Spaces (Sec. 5.2 Part 1)
Oxford Linear Algebra: Inner Product Space
Ch 4: What is an inner product? | Maths of Quantum Mechanics
Inner Products in Hilbert Space
Inner Product Spaces - 1
Inner Products and Inner Product Spaces | Linear Algebra
Dot products and duality | Chapter 9, Essence of linear algebra
MA1101 Module 5 Video 1: Inner Product Spaces
Linear Algebra- Inner Product on Space of Continuous Functions
Linear Algebra 6.1.1 Inner Product, Vector Length and Distance
Basics of Inner Product Spaces
Angle and Orthogonality in Inner Product Spaces #1 | Linear Algebra Lumist
Introduction to Inner Product Spaces
An introduction to inner product space (Part 1)
Inner Product Spaces
Inner Product Spaces Part 1
Lecture 1 (Part 4): Constructing the orthonormal basis for inner product spaces; Linear functionals
topic: inner product space ( definition & properties) ....
The Gram-Schmidt Process
Inner Product | Inner Product Space - Concept & Properties of Inner Product | Liner Algebra
Linear Algebra: inner product spaces and norms, 4-1-19
Inner Product Spaces - 7 (Gram-Schmidt Process -1)
Orthogonal and Orthonormal Sets in Inner Product Spaces | Linear Algebra
1.LINEAR ALGEBRA | DOT (INNER) PRODUCT, ORTHOGONALITY, NORM | UNIT -1 | #csirnet #mat #linearalgebra
Комментарии
 0:23:02
0:23:02
 0:34:12
0:34:12
 0:10:11
0:10:11
 0:08:41
0:08:41
 0:38:12
0:38:12
 0:20:59
0:20:59
 0:14:12
0:14:12
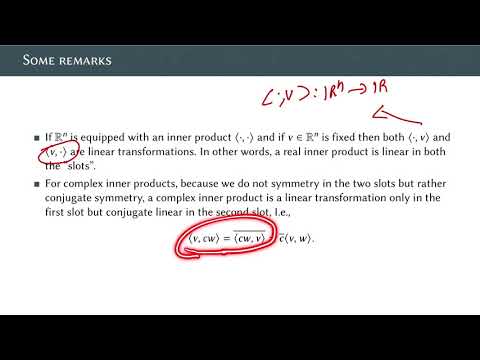 0:33:43
0:33:43
 0:07:44
0:07:44
 0:12:25
0:12:25
 0:23:09
0:23:09
 0:07:06
0:07:06
 1:08:42
1:08:42
 0:33:09
0:33:09
 0:14:12
0:14:12
 0:28:22
0:28:22
 0:30:30
0:30:30
 0:00:16
0:00:16
 0:10:07
0:10:07
 0:18:16
0:18:16
 0:49:16
0:49:16
 0:29:35
0:29:35
 0:06:49
0:06:49
 0:00:50
0:00:50