filmov
tv
17. Stochastic Processes II

Показать описание
MIT 18.S096 Topics in Mathematics with Applications in Finance, Fall 2013
Instructor: Choongbum Lee
This lecture covers stochastic processes, including continuous-time stochastic processes and standard Brownian motion.
License: Creative Commons BY-NC-SA
Instructor: Choongbum Lee
This lecture covers stochastic processes, including continuous-time stochastic processes and standard Brownian motion.
License: Creative Commons BY-NC-SA
17. Stochastic Processes II
5. Stochastic Processes I
Stochastic Processes II: Session 01
L21.3 Stochastic Processes
Phys550 Lecture 11: Stochastic Processes II
Phys550 Lecture 11: Stochastic Processes II
Stochastic Processes: Lesson 1
Stochastic Processes II: Session 04
Stochastic Processes: Lecture 07
Stochastic Processes
Analog Communications - Stochastic Processes - Intro
Math414 - Stochastic Processes - Exercises of Chapter 2
4. Stochastic Thinking
Stochastic Processes: Lecture 3
Introduction to Stochastic Processes
Stochastic Processes I: Lecture 10
Stochastic Processes 6
Math414 - Stochastic Processes - Chapter 2 - Galton-Watson processes
Stochastic Process II
Stochastic Processes part 1
Stochastic process Meaning
Actuarial Science, CT4, Stochastic Process, Part 2
Stochastic process
Karen Habermann - Stochastic processes on surfaces in 3-dimensional contact sub-Riemannian manifolds
Комментарии
 1:15:59
1:15:59
 1:17:41
1:17:41
 0:56:42
0:56:42
 0:06:21
0:06:21
 2:20:31
2:20:31
 1:21:17
1:21:17
 1:03:44
1:03:44
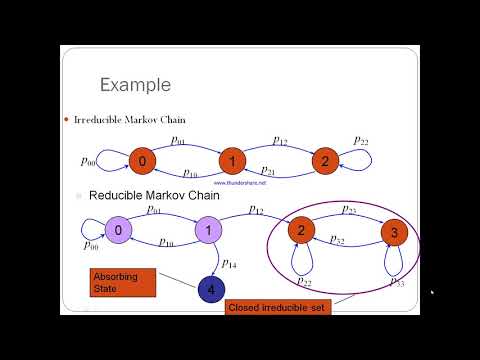 0:35:26
0:35:26
 0:44:17
0:44:17
 0:03:53
0:03:53
 0:13:20
0:13:20
 0:05:44
0:05:44
 0:49:50
0:49:50
 1:36:53
1:36:53
 0:12:37
0:12:37
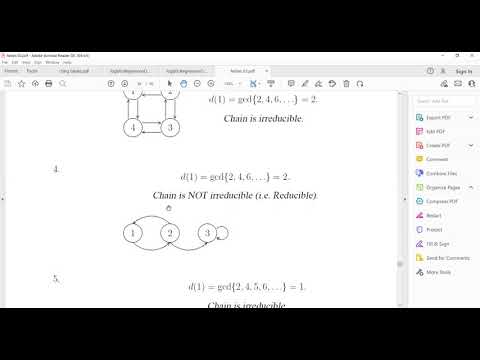 0:22:38
0:22:38
 0:39:01
0:39:01
 0:43:40
0:43:40
 0:45:31
0:45:31
 0:09:01
0:09:01
 0:00:29
0:00:29
 0:17:38
0:17:38
 0:02:10
0:02:10
 0:27:44
0:27:44