filmov
tv
Mastering Exponential Equation: Newton-Raphson and Lambert W Methods
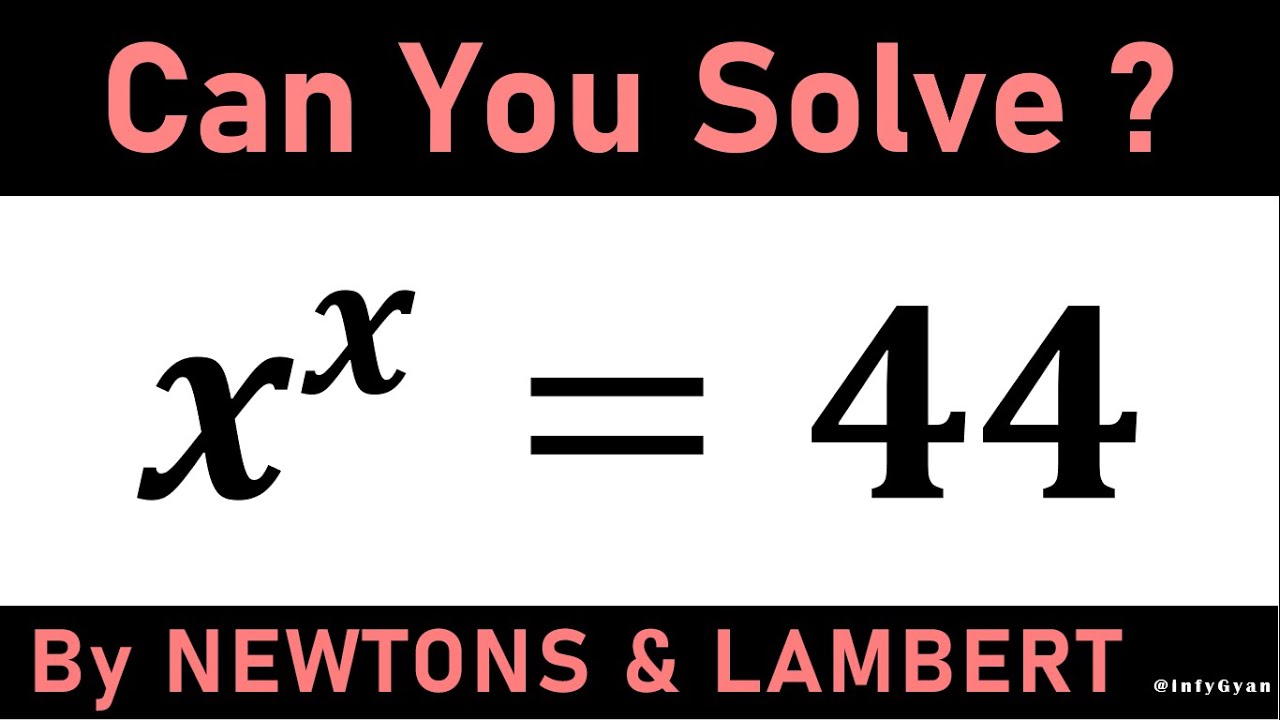
Показать описание
Mastering Exponential Equation: Newton-Raphson and Lambert W Methods
In this we'll dive into the fascinating world of exponential equations as we unveil the powerful methods of Newton-Raphson and Lambert W. In this video, we'll guide you through the step-by-step process of solving complex exponential equations using these two innovative techniques. Witness the magic of Newton-Raphson's iterative approach and the elegance of the Lambert W function as we demystify exponential equations that once seemed unsolvable. Whether you're a math enthusiast, a student struggling with exponential equations, or simply curious about advanced problem-solving methods, this video is your gateway to mastering exponential equations like never before. Join us on this enlightening journey and equip yourself with the tools to conquer exponential challenges with confidence.
Topics Covered:
1. Introduction to Exponential Equations: Understanding the basic structure and properties of exponential equations.
2. The Newton-Raphson Method: Explaining the iterative numerical method for solving equations and its application to exponential equations.
3. Lambert W Function: Introducing the Lambert W function, its definition, and its significance in solving exponential equations.
4. Solving Simple Exponential Equations: Demonstrating the application of Newton-Raphson and Lambert W methods to solve straightforward exponential equations.
5. Handling Complex Exponential Equations: Addressing more challenging exponential equations and showcasing the effectiveness of Newton-Raphson and Lambert W methods.
6. Step-by-Step Solving Process: Providing a detailed walkthrough of the solving process using both Newton-Raphson and Lambert W methods.
Comparing the Methods: Highlighting the strengths and limitations of each method and discussing scenarios where one method may be preferred over the other.
#ExponentialEquations #Mathematics #NewtonRaphson #LambertW #ProblemSolving #MathHelp #MathTutorial #EquationSolvers #MathEnthusiast #MathematicsEducation #AdvancedMath #MathematicalMethods #MathematicalTechniques #ExponentialSolutions #MathematicalProblemSolving
Don't forget to like, share & subscribe!!
Thanks for Watching!!
In this we'll dive into the fascinating world of exponential equations as we unveil the powerful methods of Newton-Raphson and Lambert W. In this video, we'll guide you through the step-by-step process of solving complex exponential equations using these two innovative techniques. Witness the magic of Newton-Raphson's iterative approach and the elegance of the Lambert W function as we demystify exponential equations that once seemed unsolvable. Whether you're a math enthusiast, a student struggling with exponential equations, or simply curious about advanced problem-solving methods, this video is your gateway to mastering exponential equations like never before. Join us on this enlightening journey and equip yourself with the tools to conquer exponential challenges with confidence.
Topics Covered:
1. Introduction to Exponential Equations: Understanding the basic structure and properties of exponential equations.
2. The Newton-Raphson Method: Explaining the iterative numerical method for solving equations and its application to exponential equations.
3. Lambert W Function: Introducing the Lambert W function, its definition, and its significance in solving exponential equations.
4. Solving Simple Exponential Equations: Demonstrating the application of Newton-Raphson and Lambert W methods to solve straightforward exponential equations.
5. Handling Complex Exponential Equations: Addressing more challenging exponential equations and showcasing the effectiveness of Newton-Raphson and Lambert W methods.
6. Step-by-Step Solving Process: Providing a detailed walkthrough of the solving process using both Newton-Raphson and Lambert W methods.
Comparing the Methods: Highlighting the strengths and limitations of each method and discussing scenarios where one method may be preferred over the other.
#ExponentialEquations #Mathematics #NewtonRaphson #LambertW #ProblemSolving #MathHelp #MathTutorial #EquationSolvers #MathEnthusiast #MathematicsEducation #AdvancedMath #MathematicalMethods #MathematicalTechniques #ExponentialSolutions #MathematicalProblemSolving
Don't forget to like, share & subscribe!!
Thanks for Watching!!
Комментарии
 0:11:34
0:11:34
 0:12:24
0:12:24
 0:10:36
0:10:36
 0:08:36
0:08:36
 0:14:23
0:14:23
 0:14:10
0:14:10
 0:09:21
0:09:21
 0:12:15
0:12:15
 0:11:59
0:11:59
 0:13:10
0:13:10
 0:08:57
0:08:57
 0:09:22
0:09:22
 0:07:04
0:07:04
 0:07:52
0:07:52
 0:12:07
0:12:07
 0:10:09
0:10:09
 0:16:48
0:16:48
 0:01:27
0:01:27
 0:04:21
0:04:21
 1:00:56
1:00:56
 0:29:38
0:29:38
 0:13:30
0:13:30
 0:11:35
0:11:35
 0:00:29
0:00:29