filmov
tv
Power system angular stability

Показать описание
Power system angular stability
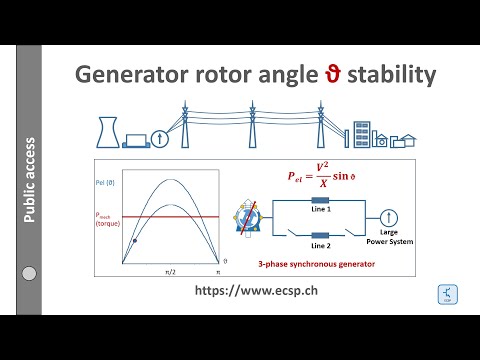
Rotor angle stability
How to feel a load angle :-)
Power system stability renewable challenge
Rotor Angle Stability in Power System for Power System Engineering Courses
Class 4 Intro Power System Stability PART I
Angular Stability Part 1: Angles in Power System and Importance
Power System Stability Studies: Equal Area Criterion
Classification of Stability - Power System Stability - Power System 3
power system angular stability formulas | Random Revision
GENERATOR : SYNCHRONIZING TORQUE AND STEADY STATE STABILITY
Power System voltage stability: The Nose Curve
Introduction to Rotor angle stability | Power System Stability Studies | Lecture-2
Angular Stability Part 2: Angular Stability in Power System
Power System Stability: Part 1 (Definition and Swing Equation)
Power system voltage stability old version
Power Grid Stability | Frequency & Voltage Stability | Rotor Angle & Converter Driven Stabil...
Comparison of Rotor Angle and Voltage Stability - Voltage Stability - Power System 3
Power system stability - power angle curve
Exp. No-2 To apply Equal area criterion for stability analysis under fault condition.
Power System Stability Lecture 22 :- Effect of Governor Action
Numerical on Transient stability
Introduction to Power System Stability for Power System Engineering Courses
Power Angle Curve in Power System (plz use speakers)
Комментарии
 0:14:37
0:14:37
 0:13:57
0:13:57
 0:00:23
0:00:23
 0:04:20
0:04:20
 0:11:37
0:11:37
 0:30:54
0:30:54
 0:08:14
0:08:14
 0:12:08
0:12:08
 0:26:17
0:26:17
 0:06:17
0:06:17
 0:07:47
0:07:47
 0:06:58
0:06:58
 0:04:18
0:04:18
 0:08:36
0:08:36
 1:15:06
1:15:06
 0:07:09
0:07:09
 0:11:49
0:11:49
 0:06:50
0:06:50
 0:36:09
0:36:09
 0:30:14
0:30:14
 0:15:42
0:15:42
 0:06:54
0:06:54
 0:12:20
0:12:20
 0:13:21
0:13:21