filmov
tv
Propositional Logic Part 8: Completeness and Compactness

Показать описание
In this video we prove the Completeness Theorem, which states that a set of sentences is consistent exactly when they have a model. We also prove the compactness theorem, which states that a set of sentences has a model if and only if every finite subset has a model.
Apologies for the section at 10:50, there is a much, much easier approach. Rewrite the implication as "not ( psi_k and not psi_i)." Now, we conclude that A cannot model "not psi_i" directly from the recursive definition of truth in a model.
0:00 Statement of the Extended Completeness Theorem
3:53 Proof that satisfiable implies consistent
5:01 Proof of a lemma
12:58 Conclusion of the proof
16:46 Proof that consistent implies satisfiable
20:20 Maximal consistent theories are closed under deduction
23:07 Inductive proof that our model satisfies
30:57 Proof of the Compactness Theorem
37:33 Conclusion of Propositional Logic
39:54 Motivation for Predicate Logic
42:59 Final note on what's to follow
Apologies for the section at 10:50, there is a much, much easier approach. Rewrite the implication as "not ( psi_k and not psi_i)." Now, we conclude that A cannot model "not psi_i" directly from the recursive definition of truth in a model.
0:00 Statement of the Extended Completeness Theorem
3:53 Proof that satisfiable implies consistent
5:01 Proof of a lemma
12:58 Conclusion of the proof
16:46 Proof that consistent implies satisfiable
20:20 Maximal consistent theories are closed under deduction
23:07 Inductive proof that our model satisfies
30:57 Proof of the Compactness Theorem
37:33 Conclusion of Propositional Logic
39:54 Motivation for Predicate Logic
42:59 Final note on what's to follow
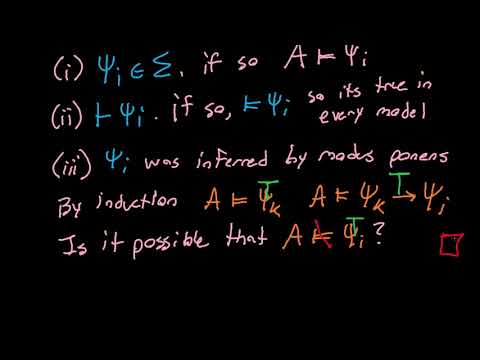 0:45:45
0:45:45
 0:58:17
0:58:17
 1:19:45
1:19:45
![[Logic] Completeness #5](https://i.ytimg.com/vi/i32F3KqV-b8/hqdefault.jpg) 0:08:36
0:08:36
 0:16:50
0:16:50
 0:39:06
0:39:06
 0:17:13
0:17:13
 0:22:54
0:22:54
 0:03:29
0:03:29
 0:57:22
0:57:22
 0:51:03
0:51:03
 0:05:25
0:05:25
 1:36:05
1:36:05
 0:42:17
0:42:17
 0:13:09
0:13:09
 0:20:17
0:20:17
 0:08:34
0:08:34
 0:12:51
0:12:51
 1:30:23
1:30:23
 0:36:47
0:36:47
 0:53:33
0:53:33
 0:32:38
0:32:38
 0:34:00
0:34:00
 0:09:34
0:09:34