Multivariable Calculus: Calculus on vector-valued functions (Curves)

A discussion of limits, continuity, differentiation, and integration of vector-valued functions r(t)=(P(t),Q(t),R(t)). The main conclusion is that we perform operations component-by-component. Around 5:45, I meant "as t approaches 3" not "as r approaches 3". (Unit 2 Lecture 2)

Key Points:
1. Limits of Vector-Valued Functions:
- Definition: The limit of a vector-valued function 𝐫(𝑡)=⟨𝑃(𝑡),𝑄(𝑡),𝑅(𝑡)⟩ as 𝑡 approaches 𝑡0 is the vector of the limits of its component functions.
- Existence: A limit exists if and only if each component limit exists.
2. Continuity of Vector-Valued Functions:
- A function is continuous at 𝑡0 if it is defined at 𝑡0 and the limit of 𝐫(𝑡) as 𝑡 approaches 𝑡0 equals 𝐫(𝑡0).
- This is determined by the continuity of each component function at 𝑡0.
3. Differentiation of Vector-Valued Functions:
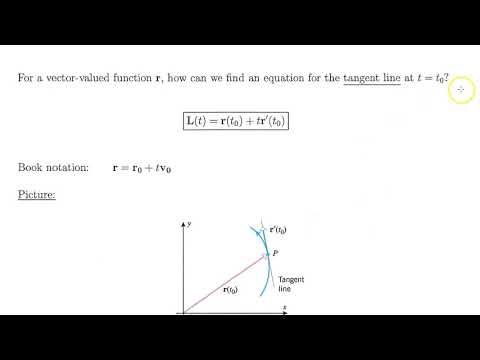
- The derivative 𝐫′(𝑡0) is the vector of the derivatives of the component functions at 𝑡0.
- Properties: We look at properties like the derivative of a constant vector, scalar multiplication, sum/difference, product rules, and chain rule.
4. Integration of Vector-Valued Functions:
- To integrate a vector-valued function over an interval, each component function is integrated over that interval.
- The antiderivative is defined similarly to single-variable calculus.
5. Smooth Curves:
- A curve is smooth if it has a differentiable parameterization with a non-zero tangent vector.

#calculus #multivariablecalculus #mathematics #iitjammathematics #calculus3 #vectorcalculus #mathtutorial

[ceosuji]

This video is so well made, thank you!!