Derivative Rules Song (Power, Product, Quotient, and Chain Rule) - AP Calc AB/BC

Derivative Rules Song (Power, Product, Quotient, and Chain Rule) - AP Calc AB/BC Unit 2

Should help you memorize the four main rules for calculating derivatives and key trig derivatives.

Made out of passion for my AP Calc class. I tried to create a genuinely educational Calc song and plan to upload more. This was not a class assignment. I just find it an effective way to study and I thought it could be creative. Apologies in advance if I sing bad. Visuals made using Final Cut Pro Apple Pencil Live Drawing on iPad.

A parody of "Riptide" by Vance Joy

Lyrics:

Verse 1:
I was scared of math and its symbols
I was scared of calculus and its rules
But then I learned the power of derivatives
And how they help me find the slopes of curves

Chorus:
The power rule's a start, simple and bright,
Lower the exponent, and get it right.
For x cubed, the derivative's in sight,
Three x squared, shining with light.

Verse 2:
When two functions meet and in product bind,
Like f(x) times g(x), what's the derivative we find?
Fear not, for the product rule unwinds,
The complexity, making it kind.

Chorus:
With the product rule, it's easy to cope,
First times derivative of second, there's hope.
Then second times derivative of first,
Like x times sine x, it's x cos x plus sine x

Bridge:
But remember trig derivatives, key to know,
Derivative of sine x is cosine x, well-known.
Cosine's derivative, negative sine x, alone,
And tangent x gives secant squared x,
For secant x, it's secant x tangent x, shown,
And cosecant x to negative cosecant x cotangent x, not overblown.
Cotangent x yields negative cosecant squared x,
These trig rules, in calculus, brightly shone.

Verse 3:
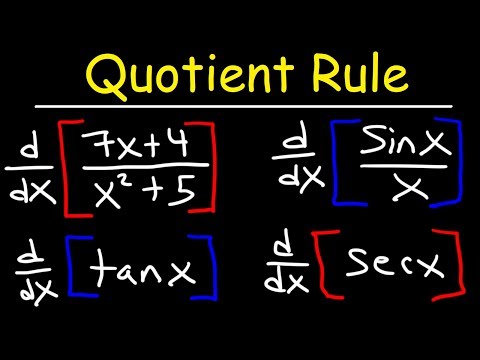
In the quotient of functions, a rule takes flight,
Like f(x) over g(x), in calculus light.
The quotient rule, a beacon so bright,
Guiding through complexities, with all its might.

Chorus:
Use the quotient rule, a trusty guide,
Bottom times derivative of top, take in stride.
Minus top by derivative of bottom, wide,
Over bottom squared, in this abide.
For x over cosine x, don't hide,
X times sine x plus cosine x, over cosine squared x, divide.

Verse 4:
When functions nest, and complexities rise,
Like f(g(x)), a common calculus guise.
The chain rule helps, a clever and wise,
Simplifying layers, under the skies.

Chorus:
Here, the chain rule, a principle sound,
First, the outer's slope, on solid ground.
The formula states, clear and unbound,
f’(g(x)) times g’(x), in synergy profound.
For instance, in sine of x squared, renowned,
Its derivative: 2x times cosine of x squared, around.

Outro:
You’re ready to rock with derivatives,
You can find the slopes of any curve,
Just remember these four rules and practice them well.