filmov
tv
Finding a closed form for ζ(4)

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
Finding a closed form from a recursively defined sequence
Determine a Closed Formula for a Given Sequence (1)
Finding A Closed Form Solution to Sn=S(n-1)+4n+5
General Methods for Finding a Closed Form (Method 5 - Expand and Contract)
48 Introduction to closed forms for sums
Example: Closed Form of a Recurrence Relation
Finding a closed form for ζ(4)
Find Closed-Form Expression for f(x) - part 1
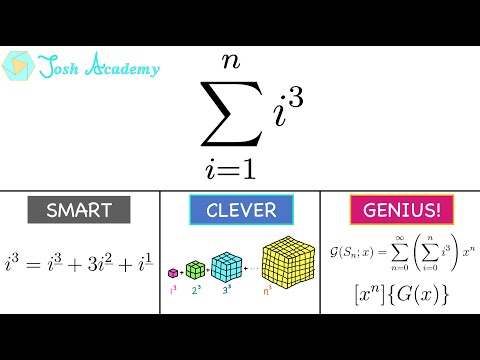
Sum of Cubes, 3 Ways
Finding a Closed Form Solution for the Towers of Hanoi
General Methods for Finding a Closed Form (Method 4 - Integration)
General Methods for Finding a Closed Form (Methods 0 - Look it Up and 1 - Guess & Prove)
General Methods for Finding a Closed Form (Method 3 - Repertoire)
General Methods for Finding a Closed Form (Method 2 - Perturb the Sum)
Find the closed form expression of a sequence by changing it to a constant-recursive sequence
Lets find a closed form of this gamma series
finding a closed form of geometric sequence
Summations 8 Using Formulas to Find Closed Form Expressions 1
Finding the closed form for a double factorial sum
Finding a closed form of a linear recurrence sequence.
How to Write in Closed Form for Summation in Sigma Notation IB HL SL AP Calculus
Sequences: closed-form formula vs recursively defined
Determine a Closed Formula for a Given Sequence (2)
Closed form from a recursive definition
Комментарии
 0:03:32
0:03:32
 0:08:05
0:08:05
 0:06:25
0:06:25
 0:10:40
0:10:40
 0:07:42
0:07:42
 0:03:02
0:03:02
 0:13:03
0:13:03
 0:00:43
0:00:43
 0:27:20
0:27:20
 0:05:39
0:05:39
 0:14:25
0:14:25
 0:13:43
0:13:43
 0:05:53
0:05:53
 0:12:09
0:12:09
 0:09:07
0:09:07
 0:13:50
0:13:50
 0:04:45
0:04:45
 0:04:09
0:04:09
 0:17:13
0:17:13
 0:10:31
0:10:31
 0:04:21
0:04:21
 0:13:13
0:13:13
 0:07:19
0:07:19
 0:05:16
0:05:16